ЬтФПФкШн
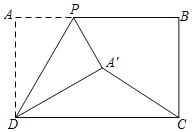
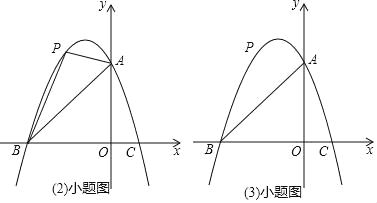
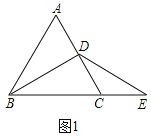
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌBDЪЧжаЯпЃЌбгГЄBCжСEЃЌЪЙCEЃНCDЃЎ

ЃЈ1ЃЉжБНгаДГі![]() ЃНЁЁ ЃЛ
ЃНЁЁ ЃЛ
ЃЈ2ЃЉНЋЭМ1жаЕФЁїBDEШЦЕуBФцЪБеыа§зЊЕНШчЭМ2ЫљЪОЮЛжУЃЌСЌНгAEЃЌPЮЊAEЕФжаЕуЃЌСЌНгPDЃЌPCЃЌЬНОПЯпЖЮPDгыPCжЎМфЕФЙиЯЕЃЛ
ЃЈ3ЃЉНЋЭМ1жаЕФЁїBDEШЦЕуBЫГЪБеыа§зЊЃЌЪЙЕуDТфдкЯпЖЮBCЩЯЃЌСЌНгAEЃЌPЮЊAEжаЕуЃЌСЌНгPDЃЎШчЭМ3ЃЌШєABЃН2![]() ЃЌЧыжБНгаДГіPDЕФГЄЮЊЁЁ ЃЎ
ЃЌЧыжБНгаДГіPDЕФГЄЮЊЁЁ ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЛЃЈ2ЃЉPCЃН![]() PDЃЌPDЁЭPCЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉPDЃН
PDЃЌPDЁЭPCЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉPDЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉжЄУїЁЯDBCЃН30ЁуЃЌЭЦГіBCЃН2CDМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉНсТлPCЃН![]() PDЃЌPDЁЭPCЃЎШчЭМ2жаЃЌбгГЄDPЕНMЪЙЕУPMЃНPDЃЌСЌНгAMЃЌCDЃЌCMЃЎжЄУїЁїDBCЁеЁїMACЃЈSASЃЉЃЌЭЦГіЁїDCMЪЧЕШБпШ§НЧаЮЃЌМДПЩНтОіЮЪЬтЃЎ
PDЃЌPDЁЭPCЃЎШчЭМ2жаЃЌбгГЄDPЕНMЪЙЕУPMЃНPDЃЌСЌНгAMЃЌCDЃЌCMЃЎжЄУїЁїDBCЁеЁїMACЃЈSASЃЉЃЌЭЦГіЁїDCMЪЧЕШБпШ§НЧаЮЃЌМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌСЌНгPCЃЌЧѓГіCDЃЌРћгУЃЈ2ЃЉжаНсТлНтОіЮЪЬтМДПЩЃЎ
ЃЈ1ЃЉжЄУїЃКШчЭМ1жаЃЌ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌBDЪЧжаЯпЃЌ
ЁрBDЁЭACЃЌЁЯABDЃНЁЯDBCЃН30ЁуЃЌЁЯACBЃН60ЁуЃЌ
ЁрBCЃН2CDЃЌ
ЁпCDЃНCEЃЌ
ЁрBCЃН2ECЃЌ
Ёр![]() ЃН2ЃЎ
ЃН2ЃЎ
ЙЪД№АИЮЊ2ЃЎ
ЃЈ2ЃЉНтЃКНсТлPCЃН![]() PDЃЌPDЁЭPCЃЎ
PDЃЌPDЁЭPCЃЎ
РэгЩЃКШчЭМ2жаЃЌбгГЄDPЕНMЪЙЕУPMЃНPDЃЌСЌНгAMЃЌCDЃЌCMЃЎ
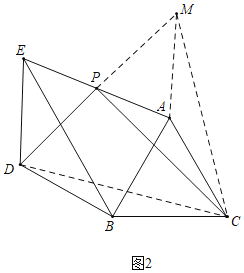
ЁпEPЃНPAЃЌЁЯEPDЃНЁЯAPMЃЌPDЃНPMЃЌ
ЁрЁїEPDЁеЁїAPMЃЈSASЃЉЃЌ
ЁрDEЃНAMЃЌЁЯDEPЃНЁЯPAMЃЌ
ЁпЁЯDBC+ЁЯACB+ЁЯCAE+ЁЯAED+ЁЯEDBЃН540ЁуЃЌ
ЁрЁЯDBC+ЁЯCAE+ЁЯAEDЃН540ЁуЉ120ЁуЉ60ЁуЃН360ЁуЃЌ
ЁпЁЯCAM+ЁЯCAE+ЁЯMAPЃН360ЁуЃЌ
ЁрЁЯCBDЃНЁЯCAMЃЌ
ЁпDEЃНDBЃНAMЃЌCBЃНCAЃЌ
ЁрЁїDBCЁеЁїMACЃЈSASЃЉЃЌ
ЁрCDЃНCMЃЌЁЯDCBЃНЁЯMACЃЌ
ЁрЁЯMCDЃНЁЯACBЃН60ЁуЃЌ
ЁрЁїDCMЪЧЕШБпШ§НЧаЮЃЌ
ЁпDPЃНPMЃЌ
ЁрPCЃН![]() PDЃЌPCЁЭPDЃЎ
PDЃЌPCЁЭPDЃЎ
ЃЈ3ЃЉНтЃКЂйШчЭМ3жаЃЌСЌНгPCЃЎ
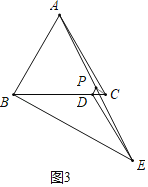
гЩЬтвтABЃНBCЃНACЃН2![]() ЃЌBDЃН3
ЃЌBDЃН3
ЁрCDЃНBCЉBDЃН2![]() Љ3ЃЌ
Љ3ЃЌ
гЩЃЈ2ЃЉПЩжЊЁЯCPDЃН90ЁуЃЌЁЯPCDЃН30ЁуЃЌ
ЁрPDЃН![]() CDЃН
CDЃН![]() Љ
Љ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊ![]() Љ
Љ![]() ЃЎ
ЃЎ