题目内容
通过阅读所得的启示,回答问题(阅读中的结论可以直接使用).
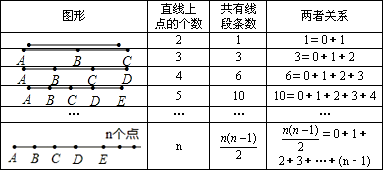
阅读:在直线上有n个不同的点,则此图中共有多少条线段?
通过画图尝试,我们发现了如下的规律:
问题:(1)某学校七年级共有8个班级进行辩论比赛,规定采用单循环赛制(每两个班之间赛一场),请问该校七年级的辩论赛共需进行多少场辩论赛?
(2)往返上海与北京之间的某趟火车,共有15个车站(包括上海与北京),则共需要准备多少种不同的车票?
阅读:在直线上有n个不同的点,则此图中共有多少条线段?
通过画图尝试,我们发现了如下的规律:
| 图形 | 直线上点的个数 | 共有线段条数 | 两者关系 | ||||
 |
2 | 1 | 1=0+1 | ||||
 |
3 | 3 | 3=0+1+2 | ||||
 |
4 | 6 | 6=0+1+2+3 | ||||
 |
5 | 10 | 10=0+1+2+3+4 | ||||
| … | … | … | … | ||||
 |
n |
|
|
(2)往返上海与北京之间的某趟火车,共有15个车站(包括上海与北京),则共需要准备多少种不同的车票?
分析:(1)把每一个班级看作一个点,利用图表公式列式进行计算即可得解;
(2)把15个车站看作15个点,求出线段的条数,再考虑车票有起点与终点站之分乘以2,即可得解.
(2)把15个车站看作15个点,求出线段的条数,再考虑车票有起点与终点站之分乘以2,即可得解.
解答:解:(1)把每一个班级看作一个点,则
=28场;
(2)15个车站看作15个点,线段条数为
=105,
因为车票有起点和终点站之分,
所以车票要2×105=210种.
| 8×(8-1) |
| 2 |
(2)15个车站看作15个点,线段条数为
| 15×(15-1) |
| 2 |
因为车票有起点和终点站之分,
所以车票要2×105=210种.
点评:本题是对图形变化规律,理解并应用图表数据中线段上点的个数与线段的条数的公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
通过阅读所得的启示,回答问题(阅读中的结论可以直接使用).
阅读:在直线上有n个不同的点,则此图中共有多少条线段?
通过画图尝试,我们发现了如下的规律:
| 图形 | 直线上点的个数 | 共有线段条数 | 两者关系 |
 | 2 | 1 | 1=0+1 |
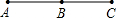 | 3 | 3 | 3=0+1+2 |
 | 4 | 6 | 6=0+1+2+3 |
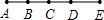 | 5 | 10 | 10=0+1+2+3+4 |
| … | … | … | … |
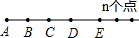 | n |  |  =0+1+2+3+…+(n-1) =0+1+2+3+…+(n-1) |
(2)往返上海与北京之间的某趟火车,共有15个车站(包括上海与北京),则共需要准备多少种不同的车票?