题目内容
（2013•黄石）若关于x的函数y=kx2+2x-1与x轴仅有一个公共点，则实数k的值为
0或-1
0或-1
．分析：令y=0，则关于x的方程kx2+2x-1=0只有一个根，所以k=0或根的判别式△=0，借助于方程可以求得实数k的值．
解答：解：令y=0，则kx2+2x-1=0．
∵关于x的函数y=kx2+2x-1与x轴仅有一个公共点，
∴关于x的方程kx2+2x-1=0只有一个根．
①当k=0时，2x-1=0，即x=
，∴原方程只有一个根，∴k=0符号题意；
②当k≠0时，△=4+4k=0，
解得，k=-1．
综上所述，k=0或-1．
故答案是：0或-1．
∵关于x的函数y=kx2+2x-1与x轴仅有一个公共点，
∴关于x的方程kx2+2x-1=0只有一个根．
①当k=0时，2x-1=0，即x=
| 1 |
| 2 |
②当k≠0时，△=4+4k=0，
解得，k=-1．
综上所述，k=0或-1．
故答案是：0或-1．
点评：本题考查了抛物线与x轴的交点．解题时，需要对函数y=kx2+2x-1进行分类讨论：一次函数和二次函数时，满足条件的k的值．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
（2013•黄石）如图，已知某容器都是由上下两个相同的圆锥和中间一个与圆锥同底等高的圆柱组合而成，若往此容器中注水，设注入水的体积为y，高度为x，则y关于x的函数图象大致是（ ）
未完成的频率分布表和频率分布直方图．请回答下列问题：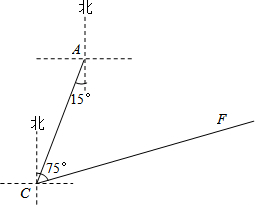
（2013•黄石）高考英语听力测试期间，需要杜绝考点周围的噪音．如图，点A是某市一高考考点，在位于A考点南偏西15°方向距离125米的C处有一消防队．在听力考试期间，消防队突然接到报警电话，告知在位于C点北偏东75°方向的F点处突发火灾，消防队必须立即赶往救火．已知消防车的警报声传播半径为100米，若消防车的警报声对听力测试造成影响，则消防车必须改进行驶，试问：消防车是否需要改道行驶？请说明理由．（