题目内容
已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为
- A.12
- B.-6
- C.-6或-12
- D.6或12
C
分析:根据一次函数的性质,分k>0和k<0时两种情况讨论求解.
解答:(1)当k>0时,y随x的增大而增大,即一次函数为增函数,
∴当x=0时,y=-2,当x=2时,y=4,
代入一次函数解析式y=kx+b得: ,
,
解得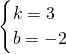 ,
,
∴kb=3×(-2)=-6;
(2)当k<0时,y随x的增大而减小,即一次函数为减函数,
∴当x=0时,y=4,当x=2时,y=-2,
代入一次函数解析式y=kx+b得: ,
,
解得 ,
,
∴kb=-3×4=-12.
所以kb的值为-6或-12.
故选C.
点评:本题要注意根据一次函数图象的性质要分情况讨论,有一定难度.
分析:根据一次函数的性质,分k>0和k<0时两种情况讨论求解.
解答:(1)当k>0时,y随x的增大而增大,即一次函数为增函数,
∴当x=0时,y=-2,当x=2时,y=4,
代入一次函数解析式y=kx+b得:
 ,
,解得
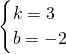 ,
,∴kb=3×(-2)=-6;
(2)当k<0时,y随x的增大而减小,即一次函数为减函数,
∴当x=0时,y=4,当x=2时,y=-2,
代入一次函数解析式y=kx+b得:
 ,
,解得
 ,
,∴kb=-3×4=-12.
所以kb的值为-6或-12.
故选C.
点评:本题要注意根据一次函数图象的性质要分情况讨论,有一定难度.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.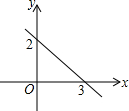 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.