题目内容
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.

1.求证:DE是⊙O的切线
2.若⊙O的半径为2,BE=1,求∠A的度数;
3.在(2)的条件下,求图形中阴影部分的面积.
1.连结AD,OD,
∵AC是直径,
∴AD⊥BC,
∵AB=AC,
∴D是BC的中点.
又∵O是AC的中点,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥DE,
又∵点D在⊙O上,
∴DE是⊙O的切线.
2.60°。
3.![]()
解析:证明:(1)连结AD,OD,
∵AC是直径,
∴AD⊥BC,
∵AB=AC,
∴D是BC的中点.
又∵O是AC的中点,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥DE,
又∵点D在⊙O上,
∴DE是⊙O的切线.
(2)60°。 (3)![]()

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
 如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是
如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )
(2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )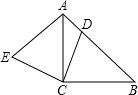 已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.
已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.