题目内容
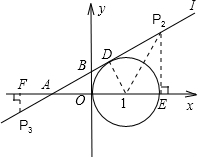
已知:如图,在直角坐标系中,⊙C与y轴相切,且C点的坐标为(1,0),直线l过点A(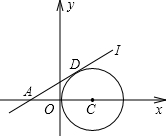 -1,0)与⊙C切于D点.
-1,0)与⊙C切于D点.
(1)求直线l的解析式;
(2)在直线l上存在点P,使△APC为等腰三角形,求P点的坐标.
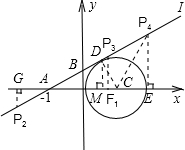 解:(1)如图①,设直线l的解析式是y=kx+b,
解:(1)如图①,设直线l的解析式是y=kx+b,连接DC,则∠ADC=90°,DC=1,AC=2,
∵△DOC为等边三角形,
∴∠DAC=30°;
设l与y轴的交点为B(0,y),则y=OAtan30°=
 .
.由B(0,
 ),A(-1,0);
),A(-1,0);用待定系数法求得直线的解析式是y=
 x+
x+ ,
,或设D(x0,y0),作DM⊥x轴于M,
在Rt△ADC中:AD=
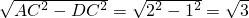
y0=
 AD=
AD= ,AM=AD•cos30°=
,AM=AD•cos30°= ,
,x0=
 -1=
-1= ,
,由D(
 ,
, )与S(-1,0),
)与S(-1,0),用待定系数法求解直线的解析式是:y=
 x+
x+
(2)方法一:如图①.
①∵B在AC的垂直平分线上,∴△ABC为等腰三角形,
∴B即为所求的一个点P,即P1(0,
 )
)②设P2(x2,y2)在直线l上,∵△CAP2为等腰三角形,
∴作P2G⊥x轴于G.在Rt△AGP2中,∵∠GAP2=30°,∴P2G=
 AP2=1
AP2=1∴AG=
 ,∴P2(-
,∴P2(- -1,-1)
-1,-1)③设P3(x3,y3)在直线l上,∵△CAP3为等腰三角形,∴P3A=AC.
作P3F=
 P3A=1,AF=P3Fcot30°=
P3A=1,AF=P3Fcot30°= .∴P3(
.∴P3( -1,1)
-1,1)④设P4(x4,y4)在直线l上,连P4C,
∵△CAP4为等腰三角形,
∴P4C=CA=2;
作P4E’⊥x轴于E’,可证E’和E重合.
在Rt△P4CE中,P4C=2∠P4CE=60°,
∴CE=
 P4C=1,P4E=
P4C=1,P4E= ,
,∴P4(2,
 ),
),∴所求的点P有4个,坐标分别是(0,
 ),(-
),(- -1,1),
-1,1),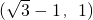 ,(2,
,(2, )
)方法二:如图②
 设P2(x2,y2)在l上,
设P2(x2,y2)在l上,∴P2满足l的解析式,
则P2(x2,
 x2+
x2+ ),且△CAP2为等腰三角形,
),且△CAP2为等腰三角形,∴P2C=AC=2,
作P2E’⊥x轴于E’,可证E’和E重合,在Rt△P2CE中,
(x2-1)2+[
 (x2+1)]2=22,
(x2+1)]2=22,解之,得x2=2或x2=-1;
而x2=-1不合题意,舍去,
∴P2(2,
 ).
).③设P3(x3,y3)在l上,
∴P3满足l的解析式.则P3(x3,
 x3+
x3+ ),
),且△CAP3为等腰三角形,∴P3A=AC=2;
作P3F⊥x轴于F.在Rt△P3FA中,(-1-x3)2+[
 (x3+1)]2=22,
(x3+1)]2=22,(x3+1)2+
 (x3+1)2=4;
(x3+1)2=4;解之,得x3=
 -1,或x3=-
-1,或x3=- -1,
-1,∴满足△CAP3为等腰三角形的点P3有两个,
即P3(
 -1,1)或(-
-1,1)或(- -1,-1);
-1,-1);∴所求的点P有4个,坐标分别是(0,
 ),(2,
),(2, ),(
),( -1,1),(-
-1,1),(- -1,-1).
-1,-1).分析:(1)根据题意,设直线l的解析式是y=kx+b,由三角形的有关性质可得A、B的坐标,用待定系数法容易求得直线的解析式,
(2)根据题意,B在AC的垂直平分线上,故△ABC为等腰三角形,由等腰三角形的性质,易得答案.
点评:此题把一次函数与三角形、圆相结合,考查了同学们综合运用所学知识的能力,是一道综合性较好的题目,有一定的难度.

练习册系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.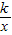 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
