题目内容
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为 .
【答案】分析:过P作PE⊥OM于E,根据垂线段最短,得出当Q与E重合时,PQ最小,根据角平分线性质求出PE=PA,即可求出答案.
解答:解:过P作PE⊥OM于E,当Q与E重合时,PQ最小,
∵PE⊥OM,PA⊥ON,OP平分∠MON,
∴PE=PM=2,
即PQ的最小值是2,
故答案为:2.
点评:本题考查了垂线段最短和角平分线的性质的应用,能根据题意得出PQ最小时Q的位置是解此题的关键,此题主要培养学生的理解能力.
解答:解:过P作PE⊥OM于E,当Q与E重合时,PQ最小,
∵PE⊥OM,PA⊥ON,OP平分∠MON,

∴PE=PM=2,
即PQ的最小值是2,
故答案为:2.
点评:本题考查了垂线段最短和角平分线的性质的应用,能根据题意得出PQ最小时Q的位置是解此题的关键,此题主要培养学生的理解能力.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 7、如图,P为∠AOB的平分线OC上任意一点,PM⊥OA于M,PN⊥OB于N,连接MN交OP于点D、则①PM=PN,②MO=NO,③OP⊥MN,④MD=ND、其中正确的有( )
7、如图,P为∠AOB的平分线OC上任意一点,PM⊥OA于M,PN⊥OB于N,连接MN交OP于点D、则①PM=PN,②MO=NO,③OP⊥MN,④MD=ND、其中正确的有( )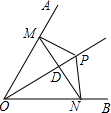 如图,P为∠AOB的平分线OC上任意一点,PM⊥OA于M,PN⊥OB于N,连接MN交OP于点D.则①PM=PN,②MO=NO,③OP⊥MN,④MD=ND.其中正确的有
如图,P为∠AOB的平分线OC上任意一点,PM⊥OA于M,PN⊥OB于N,连接MN交OP于点D.则①PM=PN,②MO=NO,③OP⊥MN,④MD=ND.其中正确的有