题目内容
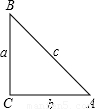
(2008•庆阳)附加题:如图,在Rt△ABC中,BC、AC、AB三边的长分别为a、b、c,则sinA= ,cosA=
,cosA= ,tanA=
,tanA= .我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
【答案】分析:利用锐角三角函数的概念:sinA= ,cosA=
,cosA= ,tanA=
,tanA= 对(1)sin2A+cos2A=1;(2)用tanA=
对(1)sin2A+cos2A=1;(2)用tanA= 进行证明.
进行证明.
解答:解:存在的一般关系有:
(1)sin2A+cos2A=1;
(2)tanA= .
.
证明:(1)∵sinA= ,cosA=
,cosA= ,
,
a2+b2=c2,
∴sin2A+cos2A= =1.
=1.
(2)∵sinA= ,cosA=
,cosA= ,
,
∴tanA= =
= ,
,
= .
.
点评:本题通过利用勾股定理和锐角三角函数的概念来对锐角的一般关系:
(1)sin2A+cos2A=1;(2)tanA= 的证明推导.
的证明推导.
 ,cosA=
,cosA= ,tanA=
,tanA= 对(1)sin2A+cos2A=1;(2)用tanA=
对(1)sin2A+cos2A=1;(2)用tanA= 进行证明.
进行证明.解答:解:存在的一般关系有:
(1)sin2A+cos2A=1;
(2)tanA=
 .
.证明:(1)∵sinA=
 ,cosA=
,cosA= ,
,a2+b2=c2,
∴sin2A+cos2A=
 =1.
=1.(2)∵sinA=
 ,cosA=
,cosA= ,
,∴tanA=
 =
= ,
,=
 .
.点评:本题通过利用勾股定理和锐角三角函数的概念来对锐角的一般关系:
(1)sin2A+cos2A=1;(2)tanA=
 的证明推导.
的证明推导. 
练习册系列答案
相关题目
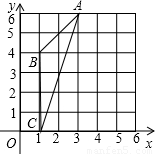
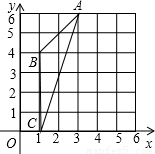
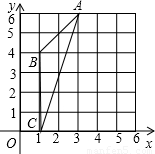
(2008•庆阳)附加题:对于本试卷第19题:“图中△ABC外接圆的圆心坐标是”.请再求:
(1)该圆圆心到弦AC的距离;
(2)以BC为旋转轴,将△ABC旋转一周所得几何体的全面积.(所有表面面积之和)
(1)该圆圆心到弦AC的距离;
(2)以BC为旋转轴,将△ABC旋转一周所得几何体的全面积.(所有表面面积之和)

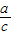 ,cosA=
,cosA=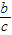 ,tanA=
,tanA=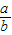 .我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.
.我们不难发现:sin260°+cos260°=1,…试探求sinA、cosA、tanA之间存在的一般关系,并说明理由.