题目内容
17.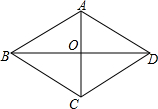 如图,已知菱形ABCD的边长为6cm,∠BAD=120°,对角线AC和BD相交于点O,求这个菱形的两条对角线和面积.
如图,已知菱形ABCD的边长为6cm,∠BAD=120°,对角线AC和BD相交于点O,求这个菱形的两条对角线和面积.
分析 利用已知条件易求AC的长,再由勾股定理可求出BO的长,进而可求对角线BD的长,利用菱形的面积等于其对角线积的一半,即可求得面积.
解答 解:在菱形ABCD中,AB=AD=6,∠BAD=120°,
∴∠ABD=30°,
∵AC⊥BD,
∴AO=$\frac{1}{2}$AB=3,AC=2AO=6(cm).
在Rt△AOB中,BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=3$\sqrt{3}$.BD=2BO=6$\sqrt{3}$(cm).
∴这个菱形的面积为$\frac{1}{2}$×6×6$\sqrt{3}$=18$\sqrt{3}$(cm2).
点评 本题主要考查的是菱形的性质:菱形的四条边都相等;对角线互相垂直平分;每条对角线平分一组对角.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
8.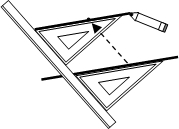 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )| A. | 两直线平行,同位角相等 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 同位角相等,两直线平行 |
12.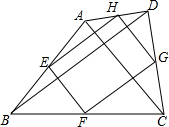 如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFCH为矩形,则四边形ABCD一定满足( )
如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFCH为矩形,则四边形ABCD一定满足( )
 如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFCH为矩形,则四边形ABCD一定满足( )
如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFCH为矩形,则四边形ABCD一定满足( )| A. | AC⊥BD | B. | AD∥BC | C. | AC=BD | D. | AB=CD |
9.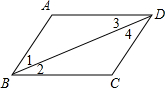 在如图中,下列能判定AD∥BC是( )
在如图中,下列能判定AD∥BC是( )
 在如图中,下列能判定AD∥BC是( )
在如图中,下列能判定AD∥BC是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠2=∠3 | D. | ∠1=∠4 |
7.边长分别等于6cm、8cm、10cm的三角形的内切圆的半径为( )cm.
| A. | $\sqrt{3}$ | B. | 2 | C. | 3$\sqrt{2}$ | D. | 6 |
 如图,点D、E、F分别在△ABC的三边上,DE∥AC,DF∥AB,已知∠1=55°,则∠2=55°.
如图,点D、E、F分别在△ABC的三边上,DE∥AC,DF∥AB,已知∠1=55°,则∠2=55°.