题目内容
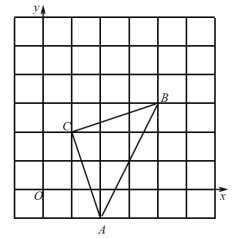
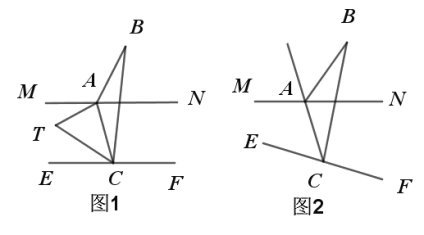
【题目】已知点A和点C分别在直线MN和直线EF上,点B在直线外,∠BAN=α,∠BCF=β.
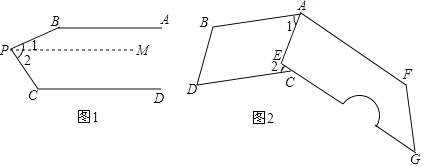
(1)如图1,若MN∥EF,则∠B= (用α,β的式子表示,不写证明过程)
(2)在(1)的条件下,点T在直线MN与直线EF之间,∠MAT=![]() ∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
∠BAN,∠TCB=2∠TCE,求∠B与∠T之间的数量关系.
(3)如图2,若MN不平行于EF,直线AC平分∠MAB,且平分∠ECB,则∠B= (用α,β的式子表示,不写证明过程)
【答案】(1)β-α;(2)∠ATC=-![]() ∠B+60°;(3)∠B=
∠B+60°;(3)∠B=![]() (β-α)
(β-α)
【解析】
(1)利用平行线的性质和三角形外角的性质求解即可;
(2)过T作TK∥MN,根据平行线的性质得出∠ATK=∠MAT,∠KTC=∠TCE,再由∠MAT=![]() ∠BAN,∠TCB=2∠TCE,表示出∠ATC=-
∠BAN,∠TCB=2∠TCE,表示出∠ATC=-![]() (β-α)+60°,结合∠B=β-α,即可求出结果;
(β-α)+60°,结合∠B=β-α,即可求出结果;
(3)根据题中条件可得:∠BAH=![]() (180°-α),∠BCA=
(180°-α),∠BCA=![]() (180°-β),结合∠BAH=∠B+∠BCA,可得∠B.
(180°-β),结合∠BAH=∠B+∠BCA,可得∠B.
解:(1)如图,设MN与BC交于点G,
∵MN∥EF,
∴∠BGN=∠BCF=β,
∴∠B=∠BGN-∠BAN=β-α,
故答案为:β-α;
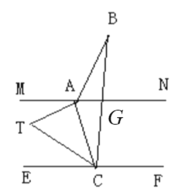
(2)如图,过T作TK∥MN,
∵MN∥EF,
∴∠ATK=∠MAT,∠KTC=∠TCE,
∵∠MAT=![]() ∠BAN,∠TCB=2∠TCE,
∠BAN,∠TCB=2∠TCE,
∴∠ATC=∠ATK+∠KTC
=∠MAT+∠TCE
=![]() ∠BAN+
∠BAN+![]() ∠TCB
∠TCB
=![]() α+
α+![]() ×
×![]() ×(180°-∠BCF)
×(180°-∠BCF)
=![]() α-
α-![]() β+60°
β+60°
=-![]() (β-α)+60°
(β-α)+60°
∵∠B=β-α,
∴∠ATC=-![]() ∠B+60°;
∠B+60°;
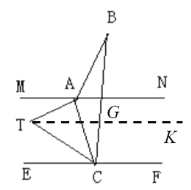
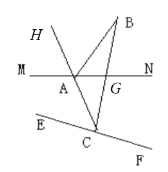
(3)如图,
∵直线AC平分∠MAB,且平分∠ECB,
∴∠BAH=∠MAH=![]() (180°-∠BAN)=
(180°-∠BAN)=![]() (180°-α),
(180°-α),
∠BCA=∠ECA=![]() (180°-∠BCF)=
(180°-∠BCF)=![]() (180°-β),
(180°-β),
∵∠BAH=∠B+∠BCA,
∴![]() (180°-α)=∠B+
(180°-α)=∠B+![]() (180°-β),
(180°-β),
∴∠B=![]() (β-α).
(β-α).

 阅读快车系列答案
阅读快车系列答案【题目】为了鼓励市民节约用水,万州市居民生活用水按阶梯式水价计费,表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:(水价计费![]() 自来水销售费用
自来水销售费用![]() 污水处理费用)
污水处理费用)
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元 | 单价:元 |
17吨及以下 |
| 0.80 |
超过17吨不超过30吨的部分 |
| 0.80 |
超过30吨的部分 | 6.00 | 0.80 |
说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费;
已知小明家2013年3月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求![]() ,
,![]() 的值.
的值.
(2)随着夏天的到来,用水量将增加。为了节省开支,小梦计划把6月份的水费控制在不超过家庭月收入的2%,若小梦加的月收入为9200元,则小王家6月份最多能用水多少吨?