Question

【题目】如图，在平面直角坐标系中，抛物线与轴交于两点，点．

(1)当时，求抛物线的顶点坐标及线段的长度；

(2)若点关于点的对称点恰好也落在抛物线上，求的值．

Answer 1

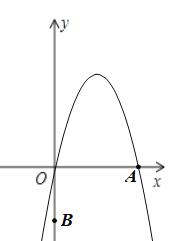
【答案】（1）顶点坐标为（3，9），OA=6；（2）m=2

【解析】

（1）把m代入抛物线，根据二次函数的图像与性质即可求出顶点，与x轴的交点，即可求解；

（2）先用含m的式子表示A点坐标，再根据对称性得到A’的坐标，再代入抛物线即可求出m的值．

解：（1）当y=0时，

，

即O（0，0），A（6，0）

∴OA=6

把x=3代入 y=-32+69

∴顶点坐标为（3，9）

（2）当y=0时，

，

即A（m，0）

∵点A关于点B的对称点A′

∴A′(-m，-8)

把A′(-m，-8)代入得m1=2,m2=-2（舍去）

∴m=2.