题目内容
已知在△ABC中,∠BAC=90°,AC=4,BC= ,若点D、E、F分别为AB、BC、AC边的中点,点P为AB边上的一个动点(且不与点A、B重合),PQ∥AC,且交BC于点Q,以PQ为一边在点B的异侧作正方形PQMN,设正方形PQMN与矩形ADEF的公共部分的面积为S,BP的长为x,试求S与x之间的函数关系式.
,若点D、E、F分别为AB、BC、AC边的中点,点P为AB边上的一个动点(且不与点A、B重合),PQ∥AC,且交BC于点Q,以PQ为一边在点B的异侧作正方形PQMN,设正方形PQMN与矩形ADEF的公共部分的面积为S,BP的长为x,试求S与x之间的函数关系式.

解:根据AC,BC的长,可在直角三角形中求出AB=8,那么DE=2,AD=BD=4,要分四种情况进行讨论:
①当N在D点或D点左侧时,即0<x≤
 时,此时正方形与矩形没有重合,因此S=0
时,此时正方形与矩形没有重合,因此S=0②当N在D点右侧,而P点在D点左侧时,即
 <x≤4,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN-PD=PN-(BD-BP)=
<x≤4,此时正方形与矩形重合的面积应该是以DN为长,NM为宽的矩形,DN=PN-PD=PN-(BD-BP)= x-(4-x)=
x-(4-x)= x-4,而NM=PQ=
x-4,而NM=PQ= x,因此重合部分的面积应该是S=(
x,因此重合部分的面积应该是S=( x-4)×
x-4)× x=
x= x2-2x
x2-2x③当P在D点右侧,而N点在A点左侧时,即4<x≤
 时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN=
时,此时正方形重合部分的面积应该是以正方形边长为长,DE为宽的矩形的面积,PN= x,DE=2,因此此时重合部分的面积是S=
x,DE=2,因此此时重合部分的面积是S= x×2=x
x×2=x④当P在A左侧,而N点在BA延长线上时,即
 <x<8时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.AP=AB-BP=8-x,AF=DE=2,因此此时重合部分的面积应该是S=(8-x)×2=16-2x.
<x<8时,此时重合部分的面积应该是以DE长为宽,PA长为长的矩形的面积.AP=AB-BP=8-x,AF=DE=2,因此此时重合部分的面积应该是S=(8-x)×2=16-2x.分析:根据AC,BC的长,可在直角三角形中求出AB=8,那么DE=2,AD=BD=4,要分①当N在D点或D点左侧;②当N在D点右侧,而P点在D点左侧;③当P在D点右侧;④当P在A左侧四种情况进行讨论.
点评:本题主要考查了中位线定理以及相似三角形的应用等知识点,本题要根据正方形所处的位置不同进行分类讨论,不要漏解.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.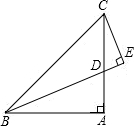 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.