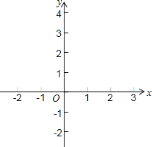Question

【题目】（题文）（题文）等边在平面直角坐标系中，已知点，将绕点O顺时针方向旋转得．

求出点B的坐标；

当与的纵坐标相同时，求出a的值；

在的条件下直接写出点的坐标．

Answer 1

【答案】(1) (2) 或 (3)或

【解析】

（1）如图1所示，过点B作BC⊥OA，垂足为C。由等边三角形的性质和特殊锐角三角函数可知OC=1，BC=，从而可求得点B的坐标；

（2）如图2所示，根据平行线的性质和旋转的定义可确定出a的值；

（3）利用旋转的性质可知A1B1=2，从而可求得B1的坐标．

如图1所示，过点B作，垂足为C．

为等边三角形，

，．

，，

．

在中，，

．

点B的坐标为

如图2所示：

点B1与点A1的纵坐标相同，

．

如图2所示：当时，点与点纵坐标相同．

如图3所示：

当时，点与点纵坐标相同．

当或时，点与点纵坐标相同．

如图2所示：由旋转的性质可知，点B的坐标为，

点的坐标为

如图3所示：由旋转的性质可知：点的坐标为

点B1的坐标为或