题目内容
H为△ABC的垂心，D，E，F分别是BC，CA，AB的中心．一个以H为圆心的⊙H交直线EF，FD，DE于A1，A2，B1，B2，C1，C2．
求证：AA1=AA2=BB1=BB2=CC1=CC2．
证明：设BC=a，CA=b，AB=c，
△ABC外接圆半径为R，⊙H的半径为r．
连HA1，AH交EF于M，
AA12=AM2+A1M2=AM2+r2-MH2
=r2+（AM2-MH2），①
又AM2-HM2=（
AH1）2-（AH-AH1）2
=AH•AH1-AH2=AH2•AB-AH2
=cosA•bc-AH2，②
而
=2R，
?AH2=4R2cos2A，
=2R，
?a2=4R2sin2A．
∴AH2+a2=4R2，AH2=4R2-a2．③
由①、②、③有
AA12=r2+
•bc-（4R2-a2）
=（a2+b2+c2）-4R2+r2．
同理，BB12=（a2+b2+c2）-4R2+r2，CC12=（a2+b2+c2）-4R2+r2．
故有AA1=BB1=CC1．
分析：只须证明AA1=BB1=CC1即可．
点评：本题考查了三角形的垂心，外心的综合运用，涉及勾股定理，正弦定理的运用，比较复杂，考查了学生分析问题的能力．
△ABC外接圆半径为R，⊙H的半径为r．
连HA1，AH交EF于M，
AA12=AM2+A1M2=AM2+r2-MH2
=r2+（AM2-MH2），①
又AM2-HM2=（
AH1）2-（AH-AH1）2=AH•AH1-AH2=AH2•AB-AH2
=cosA•bc-AH2，②
而
=2R，?AH2=4R2cos2A，
=2R，?a2=4R2sin2A．
∴AH2+a2=4R2，AH2=4R2-a2．③
由①、②、③有
AA12=r2+
•bc-（4R2-a2）=
（a2+b2+c2）-4R2+r2．同理，BB12=
（a2+b2+c2）-4R2+r2，CC12=（a2+b2+c2）-4R2+r2．故有AA1=BB1=CC1．
分析：只须证明AA1=BB1=CC1即可．
点评：本题考查了三角形的垂心，外心的综合运用，涉及勾股定理，正弦定理的运用，比较复杂，考查了学生分析问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
12、如图，点H为△ABC的垂心，以AB为直径的⊙O1和△BCH的外接圆⊙O2相交于点D，延长AD交CH于点P，
11、如图，在锐角△ABC内有一点P，直线AP，BP，CP分别交对边于Q1，Q2，Q3，且∠PQ1C=∠PQ2A=∠PQ3B．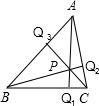
如图，在锐角△ABC内有一点P，直线AP，BP，CP分别交对边于Q1，Q2，Q3，且∠PQ1C=∠PQ2A=∠PQ3B．
