��Ŀ����
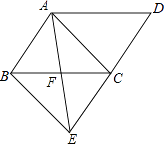
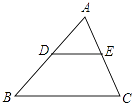
����Ŀ����֪����ͼ����Rt��ABC�У���C=90�㣬AC=8cm��BC=6cm��ֱ��PE��B���������2cm/s���ٶ����A�����˶�����ʼ����BCƽ�У���AC���ڵ�E��ͬʱ����F��C���������1cm/s���ٶ���CB���B�˶������˶�ʱ��Ϊt ��s����0��t��5����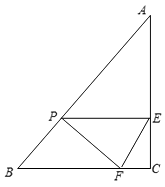
��1����tΪ��ֵʱ���ı���PFCE�Ǿ��Σ�
��2�����PEF�����ΪS��cm2������S��t�ĺ�����ϵʽ��
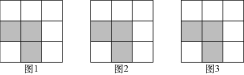
��3���Ƿ����ijһʱ��t��ʹ��PEF������ǡ�ABC����� ![]() �������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4������BE���Ƿ����ijһʱ��t��ʹPF����BE���е㣿�����ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��Rt��ABC�У��ߡ�C=90�㣬AC=8��BC=6��
��AB= ![]() =
= ![]() =10��
=10��
��PE��BC��
�� ![]() =
= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() =
= ![]() ��
��
��PE= ![]() ��10��2t����AE=
��10��2t����AE= ![]() ��10��2t����
��10��2t����
��PE=CFʱ���ı���PECF�Ǿ��Σ�
�� ![]() ��10��2t��=t��
��10��2t��=t��
���t= ![]()
��2���⣺S= ![]() PECE=
PECE= ![]() ��
�� ![]() ��10��2t����[8��
��10��2t����[8�� ![]() ��10��2t��]=��
��10��2t��]=�� ![]() t2+
t2+ ![]() t
t
��3���⣺������ڣ������⩁ ![]() t2+
t2+ ![]() t=
t= ![]() ��
�� ![]() ��6��8��
��6��8��
������t2��5t=5=0��
���t= ![]() ��
��
��t= ![]() ʱ����PEF������ǡ�ABC�����
ʱ����PEF������ǡ�ABC����� ![]()
��4���⣺��PE=BFʱ��PF����BE���е㣮
���� ![]() ��10��2t��=6��t��
��10��2t��=6��t��
���t=0���������⣬
�����ijһʱ��t��ʹPF����BE���е㣮
����������1���������ݹ��ɶ������AB�ij���Ȼ����PE��BC���ɵõ���APE�ס�ABC���������������ε����ʿɵõ�PE��t�Ĺ�ϵʽ������ɵ�PE=CFʱ���ı���PECF�Ǿ��Σ��г�������⼴�ɣ�
��2���ɣ�1���ɵõ�PE��CE�ij���Ȼ���ٸ���S=![]() ,PECE���㼴�ɣ�
,PECE���㼴�ɣ�
��3��������ڣ�Ȼ���ɡ�PEF�����=��ABC�����![]() �з�����⼴��.
�з�����⼴��.
��4����PE=BFʱ��PF����BE���е㣮����![]() ��10-2t��=6-t���Ӷ��������ж�.
��10-2t��=6-t���Ӷ��������ж�.