Question

【题目】某校数学兴趣小组在探究如何求tan15°的值，经过自主思考、合作交流讨论，得到以下思路：

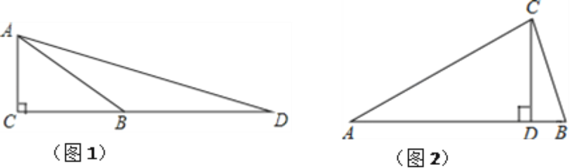
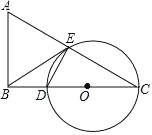
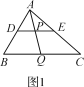
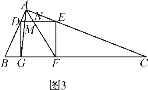
思路一 如图1，在Rt△ABC中，∠C＝90°，∠ABC＝30°，延长CB至点D，使BD＝BA，连接AD．……

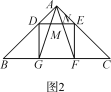
思路二 如图2，在顶角为30°的等腰三角形ABC中，AB＝AC，若过点C作CD⊥AB于点D，则∠BCD＝15°……

思路三 利用科普书上的有关公式：tan（α＋β）＝；

tan（α―β）＝；…

请解决下列问题（上述思路仅供参考）．

（1）选择你喜欢的一种思路，完成解答过程，求出tan 15°的值（保留根号）；

（2）试利用同样的方法，计算tan22.5°的值（保留根号）．

Answer 1

【答案】（1）2－ ；（2）－1

【解析】

(1)选择思路2，因为AB＝AC，∠A＝30°，CD⊥AB，可得CD＝AC，设CD＝AC＝x，根据勾股定理可得AD＝x，所以BD＝AB－AD＝2x－x＝（2－）x，从而求解.

（2）可设∠ABC=45°，因为AB＝BD，可得∠D=22，5°，设AB＝BD=。然后求出的值即可.

（1）思路2: 解：由已知AB＝AC，

∵∠A＝30°，CD⊥AB，∴CD＝AC＝x，∠BCD=90°-（180°-30°）=15°，

则AD2＝AC2－CD2＝（2x）2－x2＝3x2，∴AD＝x，

∴BD＝AB－AD＝2x－x＝（2－）x，

∴tan ∠BCD =tan15°＝＝＝2-．

（其它思路同样可以）

（2）在图1中，，设∠ABC＝45°，AB＝BD＝，

∴∠D＝∠ABC＝22.5°，∵AB＝，∠ABC＝45°，∴AC＝BC＝1，

∴CD＝1＋，

∴tan∠D=tan22.5°＝＝－1．