题目内容
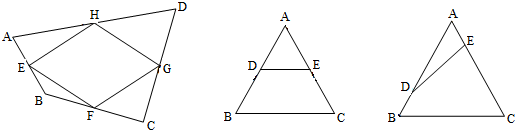
顺次连接四边形ABCD各边中点，得到四边形EFGH，要使四边形EFGH是菱形，应添加的条件是
- A.AD∥BC
- B.AC=BD
- C.AC⊥BD
- D.AD=AB
B
分析：菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：
①定义；
②四边相等；
③对角线互相垂直平分．
解答：
解：添加AC=BD．
如图，AC=BD，E、F、G、H分别是线段AB、BC、CD、AD的中点，
则EH、FG分别是△ABD、△BCD的中位线，EF、HG分别是△ACD、△ABC的中位线
∴EH=FG=
BD，EF=HG=AC，
∴当AC=BD时，
EH=FG=FG=EF成立，
则四边形EFGH是菱形．
故选B．
点评：本题考查菱形的判定和三角形中位线定理．本题是开放题，可以针对各种特殊的平行四边形的判定方法，给出条件，再证明结论．
分析：菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：
①定义；
②四边相等；
③对角线互相垂直平分．
解答：
解：添加AC=BD．如图，AC=BD，E、F、G、H分别是线段AB、BC、CD、AD的中点，
则EH、FG分别是△ABD、△BCD的中位线，EF、HG分别是△ACD、△ABC的中位线
∴EH=FG=
BD，EF=HG=AC，∴当AC=BD时，
EH=FG=FG=EF成立，
则四边形EFGH是菱形．
故选B．
点评：本题考查菱形的判定和三角形中位线定理．本题是开放题，可以针对各种特殊的平行四边形的判定方法，给出条件，再证明结论．
练习册系列答案
相关题目
如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=
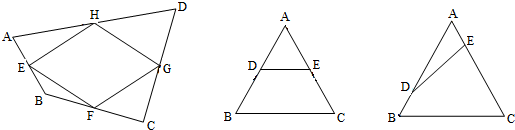
如图，在边长为1的正方形网格中，△A′B′C′与△ABC是中心对称图形．
