��Ŀ����
��ͼ��������AOCB��ƽ��ֱ������ϵ �У���OΪԭ�㣬��B�ڷ���������
�У���OΪԭ�㣬��B�ڷ��������� ��
�� ��
�� ��ͼ���ϣ���BOC�����Ϊ
��ͼ���ϣ���BOC�����Ϊ ��
��
��1���������� �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2��������E��A��ʼ��AB��B��ÿ��1����λ���ٶ��˶���ͬʱ����F ��B��ʼ��BC��C��ÿ�� ����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF�������
����λ���ٶ��˶���������һ�����㵽��˵�ʱ����һ��������ֹ֮ͣ�˶������˶�ʱ����t��ʾ����BEF������� ��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������
��ʾ�����S����t�ĺ�����ϵʽ����������˶�ʱ��tȡ��ֵʱ����BEF��������
��3�����˶�ʱ��Ϊ ��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��ʱ�������������Ƿ���ڵ�P��ʹ��PEF���ܳ���С�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�⣺��1�����ı���AOCBΪ������ ����AB=BC=OC=OA��
���B������ ��
�� ����
����
�� ����
����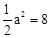 �����
�����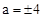 ��
��
�֡ߵ�B�ڵ�һ���ޣ����B����Ϊ��4��4����
����B��4��4������ ��
��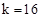 ��
��
�෴������������ʽΪ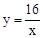 ��
��
��2�����˶�ʱ��Ϊt������E���ٶ�Ϊÿ��1����λ����F ���ٶ�Ϊÿ��2����λ��
��AE=t�� BF ��
��
��AB=4����BE=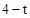 ��
��
�� ��
��
��S����t�ĺ�����ϵʽΪ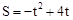 ����
���� ʱ����BEF��������
ʱ����BEF��������
��3�����ڡ�
��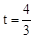 ʱ����E������Ϊ��
ʱ����E������Ϊ�� ��4������F������Ϊ��4��
��4������F��������4�� ����
����
����F����� ��ĶԳƵ�F1����F1��4��
��ĶԳƵ�F1����F1��4��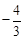 ����������E��F1��ֱ�ߣ�
����������E��F1��ֱ�ߣ�
��E ��4����F1��4��
��4����F1��4��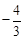 ���ɵ�ֱ��EF1�Ľ���ʽ��
���ɵ�ֱ��EF1�Ľ���ʽ�� ��
��
��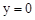 ʱ��
ʱ��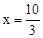 ����P�������Ϊ��
����P��������� ��0����
��0����
����E����� ��ĶԳƵ�E1����E1��
��ĶԳƵ�E1����E1��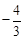 ��4����������E1��F��ֱ�ߣ�
��4����������E1��F��ֱ�ߣ�
��E1��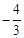 ��4����F��4��
��4����F��4�� ���ɵ�ֱ��E1F�Ľ���ʽ��
���ɵ�ֱ��E1F�Ľ���ʽ��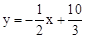 ��
��
�� ʱ��
ʱ��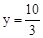 ����P�������Ϊ��0��
����P���������0�� ����
����
����������P�������ֱ�Ϊ�� ��0����0��
��0����0�� ����
����
���������������1�����������ε����ʺ͡�BOC�����Ϊ ����ʽ�����B�����꣬����
����ʽ�����B�����꣬���� ���������k���Ӷ���÷����������Ĺ�ϵʽ��
���������k���Ӷ���÷����������Ĺ�ϵʽ��
��2������˫������˶�ʱ����ٶȱ�ʾ��BF��BE���������S����t�ĺ�����ϵʽ����Ϊ����ʽ���ɸ��ݶ��κ�������ֵԭ����á�BEF��������ʱt��ֵ��
��3��������ԳƵ�ԭ������F����� ��ĶԳƵ�F1��E�����
��ĶԳƵ�F1��E����� ��ĶԳƵ�E1����������ۡ�
��ĶԳƵ�E1����������ۡ�

 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д��׳�����·��ɲ�����飬�ռ������������±���ʾ��
�ٶ� (ǧ��/ʱ) (ǧ��/ʱ) | 0 | 5 | 10 | 15 | 20 | 25 | �� |
ɲ������ (��) (��) | 0 |  | 2 |  | 6 |  | �� |
 ��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������
��Ϊ������꣬����ͼ��ʾ������ϵ�л���ɲ������ (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(ǧ��/ʱ)�ĺ���ͼ�������Ľ���ʽ��
(2)��һ������Ϊ40ǧ��/ʱ����·�ϣ��ס�������������У�ͬʱɲ������������ײ�ˣ��º��üס�������ɲ������ֱ�Ϊ12��10.5�ף���֪�ҳ�ɲ������
 (��)���ٶ�
(��)���ٶ� (ǧ��/ʱ)���㺯��
(ǧ��/ʱ)���㺯�� ������������ٶȷ��������ײԭ��
������������ٶȷ��������ײԭ��  ��ֱ��
��ֱ�� ���ڵ�O��0��0����
���ڵ�O��0��0���� ����B����������O��A֮���һ�����㣬����B�ֱ������ᡢ�����ƽ������ֱ��OA���ڵ�C��E��
����B����������O��A֮���һ�����㣬����B�ֱ������ᡢ�����ƽ������ֱ��OA���ڵ�C��E��

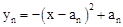 ��nΪ����������0<a1<a2<��<an����x��Ľ���ΪAn-1��bn-1,0����An(bn��0)����n=1ʱ����1��������
��nΪ����������0<a1<a2<��<an����x��Ľ���ΪAn-1��bn-1,0����An(bn��0)����n=1ʱ����1�������� ��x��Ľ���ΪA0��0��0����A1��b1��0���������������ƣ�
��x��Ľ���ΪA0��0��0����A1��b1��0���������������ƣ�

 �Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
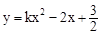 ��
�� �dz�����
�dz����� ��ֻ��һ�����㣬��
��ֻ��һ�����㣬�� ��ij������������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ���
��ij������������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ��� ��
�� ���㣬��
���㣬�� ��
�� ����
����