题目内容
 已知正方形ABCD中,E、F分别是对角线AC、BD的三等分点
已知正方形ABCD中,E、F分别是对角线AC、BD的三等分点
(1)求证:四边形BCFE是等腰梯形;
(2)若正方形ABCD的对角线长为9cm,求等腰梯形BCFE的面积.
(1)证明:∵E、F分别是对角线AC、BD的三等分点,
∴ =
= =
= ,
,
∴EF∥BC,
∴四边形BCFE是梯形,
∵E、F分别是对角线AC、BD的三等分点,AC=BD,
∴BF= BD,CE=
BD,CE= AC,
AC,
∴BF=CE,
∴四边形BCFE是等腰梯形;
(2)解:∵正方形ABCD的对角线长为9cm,
∴设正方形边长为x, =9,
=9,
x= .
.
梯形的上底为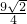 ,高为
,高为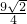 ×
× =
= ,下底为
,下底为 .
.
∴梯形的面积为: ×(
×(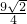 +
+ )×
)× =
=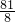 .
.
分析:(1)对角线相等的梯形是等腰梯形,根据此可判定四边形BCFE是等腰梯形.
(2)根据正方形对角线的长,可求出正方形的边长,从而可求出梯形的上底长,下底长和高,从而求出梯形的面积.
点评:本题考查正方形的性质,正方形的对角线相等和梯形的判定定理和梯形面积的求法.
∴
 =
= =
= ,
,∴EF∥BC,
∴四边形BCFE是梯形,
∵E、F分别是对角线AC、BD的三等分点,AC=BD,
∴BF=
 BD,CE=
BD,CE= AC,
AC,∴BF=CE,
∴四边形BCFE是等腰梯形;
(2)解:∵正方形ABCD的对角线长为9cm,
∴设正方形边长为x,
 =9,
=9,
x=
 .
.梯形的上底为
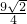 ,高为
,高为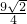 ×
× =
= ,下底为
,下底为 .
.∴梯形的面积为:
 ×(
×(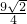 +
+ )×
)× =
=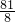 .
.分析:(1)对角线相等的梯形是等腰梯形,根据此可判定四边形BCFE是等腰梯形.
(2)根据正方形对角线的长,可求出正方形的边长,从而可求出梯形的上底长,下底长和高,从而求出梯形的面积.
点评:本题考查正方形的性质,正方形的对角线相等和梯形的判定定理和梯形面积的求法.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.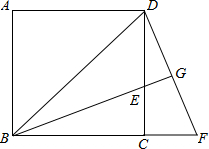 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G. 如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.