题目内容
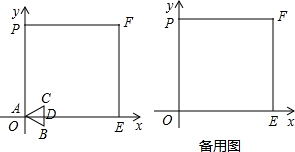 如图,将边长为8
如图,将边长为8| 3 |
(1)直接写出正方形OEFP的周长;
(2)等边△ABC的边长为2
| 3 |
分析:(1)正方形的周长等于边长的4倍,即为32
;
(2)①连接PC,根据已知条件求出三角形ACD的面积,再用含有t的代数式分别表示出三角形POA和梯形POCD的面积,利用y=S梯形PODC-S△POA-S△ADC,即可求出y与t的函数关系式;
②当P、A、B在同一直线上时(如图所示),则Rt△PBF中,∠PBF=60°,取PB的中点G,连接GF,则GF=PG=GB,则三角形BGF为等边三角形,利用勾股定理求出PB、BF的值即可求出时间t.
| 3 |
(2)①连接PC,根据已知条件求出三角形ACD的面积,再用含有t的代数式分别表示出三角形POA和梯形POCD的面积,利用y=S梯形PODC-S△POA-S△ADC,即可求出y与t的函数关系式;
②当P、A、B在同一直线上时(如图所示),则Rt△PBF中,∠PBF=60°,取PB的中点G,连接GF,则GF=PG=GB,则三角形BGF为等边三角形,利用勾股定理求出PB、BF的值即可求出时间t.
解答: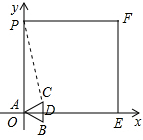 解:(1)∵边长为8
解:(1)∵边长为8
的正方形OEFP置于直角坐标系中,OE、OP分别与x轴、y轴的正半轴重合.
∴正方形OEFP的周长为:4×8
=32
;
(2)①连接PC,
∵等边△ABC的边长为2
,顶点A与坐标原点O重合,BC⊥x轴于点D,
∴AD=3,CD=
,PA=8
,
y=S梯形PODC-S△POA-S△ADC=
t+12
,
0≤t≤8
-3;
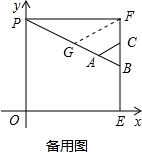 ②当A在OE上,∠BAE=∠PAO>45°,∠BAC>90°,不存在,
②当A在OE上,∠BAE=∠PAO>45°,∠BAC>90°,不存在,
当P、A、B在同一直线上时(如图所示),Rt△PBF中,∠PBF=60°,
取PB的中点G,连接GF,则GF=PG=GB,
∴△BGF是等边三角形∴BF=0.5PB,
根据勾股定理可得:PB=16,BF=8,
又∵AD=3,
∴t=8
-3+8
-8+
=17
-11,
≈18.4(秒).
 解:(1)∵边长为8
解:(1)∵边长为8| 3 |
∴正方形OEFP的周长为:4×8
| 3 |
| 3 |
(2)①连接PC,
∵等边△ABC的边长为2
| 3 |
∴AD=3,CD=
| 3 |
| 3 |
y=S梯形PODC-S△POA-S△ADC=
| ||
| 2 |
| 3 |
0≤t≤8
| 3 |
 ②当A在OE上,∠BAE=∠PAO>45°,∠BAC>90°,不存在,
②当A在OE上,∠BAE=∠PAO>45°,∠BAC>90°,不存在,当P、A、B在同一直线上时(如图所示),Rt△PBF中,∠PBF=60°,
取PB的中点G,连接GF,则GF=PG=GB,
∴△BGF是等边三角形∴BF=0.5PB,
根据勾股定理可得:PB=16,BF=8,
又∵AD=3,
∴t=8
| 3 |
| 3 |
| 3 |
| 3 |
≈18.4(秒).
点评:本题考查了正方形的性质、等边三角形的性质以及勾股定理的运用和分类讨论思想,题目综合性很强具有一定的难度.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
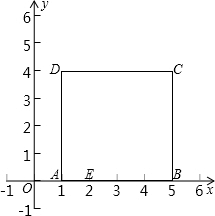 的坐标是(1,0).
的坐标是(1,0).