题目内容
【题目】线y=a(x+1)2的顶点为A,与y轴的负半轴交于点B,且OB=OA.
(1)求抛物线的解析式;
(2)若点C(-3,m)在该抛物线上,求△ABC的面积.

【答案】(1) y=-(x+1)2;(2)3.
【解析】分析:(1)由抛物线解析式确定出顶点A坐标,根据OA=OB确定出B坐标,将B坐标代入解析式求出a的值,即可确定出解析式;(2)将C坐标代入抛物线解析式求出b的值,确定出C坐标,过C作CD垂直于x轴,三角形ABC面积=梯形OBCD面积-三角形ACD面积-三角形AOB面积,求出即可.
本题解析: (1)依题意可知A(-1,0).由OB=OA,得B(0,-1).
将点B(0,-1)代入y=a(x+1)2,得-1=a(0+1)2,解得a=-1.
所以y=-(x+1)2.
(2)过C作CD⊥x轴,
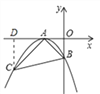
则S△ABC=S梯形OBCD-S△ACD-S△AOB=12×3×(4+1)-12×4×2-12×1×1=3.
(2)将C(-3,m)代入y=-(x+1)2,得m=-(-3+1)2,即m=-4.所以C(-3,-4).
所以S△ABC=![]() =
=![]() ×1×4+
×1×4+![]() ×1×3-
×1×3-![]() ×1×1=3.
×1×1=3.

练习册系列答案
相关题目


