题目内容
已知抛物线 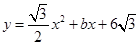 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值和点P、B的坐标;
(2)如图,在直线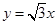 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)在 轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
(1)顶点P的坐标为(4,-2 )点B的坐标是(6,0). (2)存在;D点的坐标为(2,2
)点B的坐标是(6,0). (2)存在;D点的坐标为(2,2 )(3)可通过证明AM="AM," ∠PAM=∠BAM,AB=AP,证明△AMP≌△AMB.
)(3)可通过证明AM="AM," ∠PAM=∠BAM,AB=AP,证明△AMP≌△AMB.
解析试题分析: 解:(1)∵抛物线 经过A(2,0),
经过A(2,0),
∴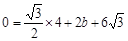 ,
,
解得 ,
,
∴抛物线的解析式为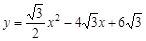 .
.
将抛物线配方,得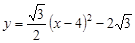 ,
,
∴顶点P的坐标为(4,-2 ).
).
令y=0,得 ,解得
,解得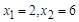 .
.
∴点B的坐标是(6,0).
(2)在直线 y= x上存在点D,使四边形OPBD为平行四边形.
x上存在点D,使四边形OPBD为平行四边形.
理由如下:设直线PB的解析式为 +b,把B(6,0),P(4,-2
+b,把B(6,0),P(4,-2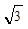 )分别代入,得
)分别代入,得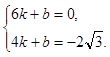
解得
∴直线PB的解析式为 .
.
又∵直线OD的解析式为 ,∴直线PB∥OD.
,∴直线PB∥OD.
解法一:设直线OP的解析式为 ,把P(4,-2
,把P(4,-2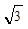 )代入,得
)代入,得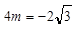 ,解得
,解得 .
.
如果OP∥BD,那么四边形OPBD为平行四边形.
设直线BD的解析式为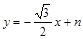 ,将B(6,0)代入,得0=
,将B(6,0)代入,得0=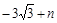 ,
,
∴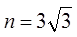
∴直线BD的解析式为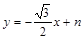 ,解方程组
,解方程组 得
得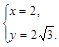
∴D点的坐标为(2,2 )
)
解法二:过点P作x轴的垂线,垂足为点C,则PC=2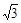 ,AC=2,
,AC=2,
由勾股定理,可得AP=4,PB=4,又∵AB=4,∴△APB是等边三角形∠PBA=∠DOB=60°,
设点D的坐标为( ,
,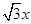 ),得
),得 =
=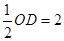 ,
,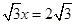
∴D点的坐标为(2,2 )
)
(3)符合条件的点M存在.
验证如下:过点P作x轴的垂线,垂足为点C,则PC=2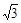 ,AC=2,
,AC=2,
由勾股定理,可得AP=4,PB=4,
又∵AB=4,∴△APB是等边三角形,作∠PAB的平分线交抛物线于M点,连接PM,BM,由于AM="AM," ∠PAM=∠BAM,AB=AP,
∴△AMP≌△AMB.
因此即存在这样的点M,使△AMP≌△AMB. 
考点:一次函数与抛物线
点评:本题难度较大,主要考查学生对一次函数和抛物线综合运用解决几何问题的能力,为中考常考题型,注意培养数形结合思想分析能力,并运用到考试中去。

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案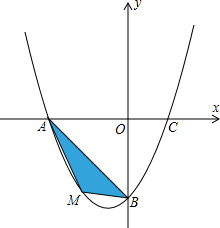 在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),
在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),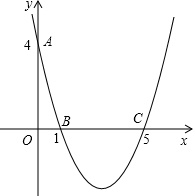 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.