题目内容
以下是2007年8月份的日历，如果用长方形所示的方法框中4个数，若它们的和为100，则这四个数中最大的一个数是________．
29
分析：由图中日历的规律可以看出同一行相邻两个数之差为1，同一列相邻两个数之差为7；所以设四个数中最大的一个数是x，则另外三个数为：x-1，x-7，x-8，由题意得出，等量关系为：这四个数的和为：100，根据等量关系列出方程即可．
解答：设四个数中最大的一个数为：x，那么另外三个数为：x-1，x-7，x-8
由题意得：x+x-1+x-7+x-8=100，
解之得：x=29
所以，这四个数中最大的一个数为：29．
点评：解题的关键在于理解日历的长方形框中4个数的关系，根据等量关系列出方程，求解．
分析：由图中日历的规律可以看出同一行相邻两个数之差为1，同一列相邻两个数之差为7；所以设四个数中最大的一个数是x，则另外三个数为：x-1，x-7，x-8，由题意得出，等量关系为：这四个数的和为：100，根据等量关系列出方程即可．
解答：设四个数中最大的一个数为：x，那么另外三个数为：x-1，x-7，x-8
由题意得：x+x-1+x-7+x-8=100，
解之得：x=29
所以，这四个数中最大的一个数为：29．
点评：解题的关键在于理解日历的长方形框中4个数的关系，根据等量关系列出方程，求解．
练习册系列答案
相关题目
小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：
| 复习日记卡片 |
| 内容：一元二次方程解法归纳 时间：2007年6月×日 |
| 举例：求一元二次方程x2-x-1=0的两个解 |
| 方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 解方程：x2-x-1=0． 解： |
方法二：利用二次函数图象与坐标轴的交点求解如图所示，把方程x2-x-1=0的解看成是二次函数y=  |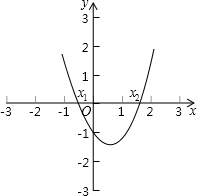
方法三：利用两个函数图象的交点求解 （1）把方程x2-x-1=0的解看成是一个二次函数y= （2）画出这两个函数的图象，用x1，x2在x轴上标出方程的解．  |
小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：
| 复习日记卡片 |
| 内容：一元二次方程解法归纳 时间：2007年6月×日 |
| 举例：求一元二次方程x2-x-1=0的两个解 |
| 方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 解方程：x2-x-1=0． 解： |
方法二：利用二次函数图象与坐标轴的交点求解如图所示，把方程x2-x-1=0的解看成是二次函数y=的图象与x轴交点的横坐标，即x1，x2就是方程的解．  |
方法三：利用两个函数图象的交点求解 （1）把方程x2-x-1=0的解看成是一个二次函数y=的图象与一个一次函数y=图象交点的横坐标； （2）画出这两个函数的图象，用x1，x2在x轴上标出方程的解．  |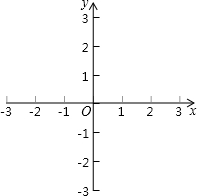
小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：
| 复习日记卡片 |
| 内容：一元二次方程解法归纳 时间：2007年6月×日 |
| 举例：求一元二次方程x2-x-1=0的两个解 |
| 方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 解方程：x2-x-1=0． 解： |
方法二：利用二次函数图象与坐标轴的交点求解如图所示，把方程x2-x-1=0的解看成是二次函数y=______的图象与x轴交点的横坐标，即x1，x2就是方程的解．  |
方法三：利用两个函数图象的交点求解 （1）把方程x2-x-1=0的解看成是一个二次函数y=______的图象与一个一次函数y=______图象交点的横坐标； （2）画出这两个函数的图象，用x1，x2在x轴上标出方程的解．  |
小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：
| 复习日记卡片 |
| 内容：一元二次方程解法归纳 时间：2007年6月×日 |
| 举例：求一元二次方程x2-x-1=0的两个解 |
| 方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 解方程：x2-x-1=0． 解： |
方法二：利用二次函数图象与坐标轴的交点求解如图所示，把方程x2-x-1=0的解看成是二次函数y=______的图象与x轴交点的横坐标，即x1，x2就是方程的解．  |
方法三：利用两个函数图象的交点求解 （1）把方程x2-x-1=0的解看成是一个二次函数y=______的图象与一个一次函数y=______图象交点的横坐标； （2）画出这两个函数的图象，用x1，x2在x轴上标出方程的解．  |
（2007•丽水）小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：
| 复习日记卡片 |
| 内容：一元二次方程解法归纳 时间：2007年6月×日 |
| 举例：求一元二次方程x2-x-1=0的两个解 |
| 方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 解方程：x2-x-1=0． 解： |
方法二：利用二次函数图象与坐标轴的交点求解如图所示，把方程x2-x-1=0的解看成是二次函数y=______的图象与x轴交点的横坐标，即x1，x2就是方程的解．  |
方法三：利用两个函数图象的交点求解 （1）把方程x2-x-1=0的解看成是一个二次函数y=______的图象与一个一次函数y=______图象交点的横坐标； （2）画出这两个函数的图象，用x1，x2在x轴上标出方程的解．  |