题目内容
【题目】如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2 ![]() 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )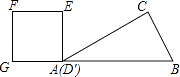
A.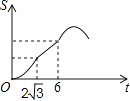
B.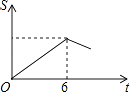
C.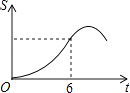
D.
【答案】A
【解析】解:如图1,CH是AB边上的高,与AB相交于点H,  ,
,
∵∠C=90°,∠BAC=30°,AB=8,
∴AC=AB×cos30°=8× ![]() =4
=4 ![]() ,BC=AB×sin30°=8×
,BC=AB×sin30°=8× ![]() =4,
=4,
∴CH=AC× ![]() ,AH=
,AH= ![]() ,(1)当0≤t≤2
,(1)当0≤t≤2 ![]() 时,
时,
S= ![]() =
= ![]() t2;(2)当2
t2;(2)当2 ![]() 时,
时,
S= ![]() ﹣
﹣ ![]()
= ![]() t2
t2 ![]() [t2﹣4
[t2﹣4 ![]() t+12]
t+12]
=2t﹣2 ![]() (3)当6<t≤8时,
(3)当6<t≤8时,
S= ![]() [(t﹣2
[(t﹣2 ![]() )tan30°
)tan30° ![]() ]×[6﹣(t﹣2
]×[6﹣(t﹣2 ![]() )]
)] ![]() ×[(8﹣t)tan60°
×[(8﹣t)tan60° ![]() ]×(t﹣6)
]×(t﹣6)
= ![]() [
[ ![]() ]×[﹣t+2
]×[﹣t+2 ![]() +6]
+6] ![]() ×[﹣
×[﹣ ![]() t
t ![]() ]×(t﹣6)
]×(t﹣6)
=﹣ ![]() t2+2t+4
t2+2t+4 ![]() ﹣
﹣ ![]() t2
t2 ![]() ﹣30
﹣30 ![]()
=﹣ ![]() t2
t2 ![]() ﹣26
﹣26 ![]()
综上,可得
S= 
∴正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是A图象.
故选:A.
【考点精析】本题主要考查了函数的图象的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案【题目】为了从甲、乙两名选手中选拔一人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
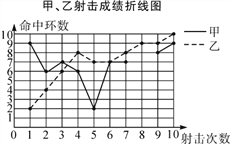
甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | |||
乙 | 1 |
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁将胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?