��Ŀ����
����Ŀ����12�֣��Ķ�������֪����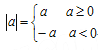 ����Ҫ�ⲻ��ʽ
����Ҫ�ⲻ��ʽ![]() �����ǿ��Է��������ȥ������ֵ���ţ�ת��Ϊ������Ϥ�IJ���ʽ��������˼·�����������½ⷨ��
�����ǿ��Է��������ȥ������ֵ���ţ�ת��Ϊ������Ϥ�IJ���ʽ��������˼·�����������½ⷨ��
�⣺��1����![]() ����
����![]() ʱ��
ʱ�� ![]()
���������ʽ���ã� ![]()
������![]() ����
����![]()
��2����![]() < 0���� x < 3ʱ��
< 0���� x < 3ʱ��![]()
���������ʽ���ã� ![]()
������x < 3���� ![]() < 3
< 3
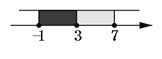
�� ��ͼ�� �ۺϣ�1������2��ԭ����ʽ�Ľ�Ϊ��![]()
��������˼�룬��̽���������2��С�⣺
��1��![]() �� ��2��
�� ��2��![]() ��
��
���𰸡�(1) ![]() ;(2)
;(2) ![]() ��
��![]() .
.
������������������������ӷ�������ۣ�ȥ����ֵ���ź��һԪһ�η��̼���.
���������
��1��![]()
��![]() ����
����![]() ʱ��
ʱ�� ![]()
���������ʽ���ã� ![]()
������![]() ����
���� ![]() ���� 2��
���� 2��
��![]() <0���� x < -1ʱ��
<0���� x < -1ʱ�� ![]()
���������ʽ���ã� ![]()
������x < -1���� ![]() < -1 ���� 4��
< -1 ���� 4��
�� �ۺ�����ԭ����ʽ�Ľ�Ϊ�� ![]() ���� 6��
���� 6��
��2��![]()
��![]() ����
����![]() ʱ��
ʱ�� ![]()
���������ʽ���ã� ![]()
������![]() ����
���� ![]() ���� 2��
���� 2��
��![]() <0���� x < 2ʱ��
<0���� x < 2ʱ�� ![]()
���������ʽ���ã� ![]()
������x < 2���� ![]() ���� 4��
���� 4��
�� �ۺ�����ԭ����ʽ�Ľ�Ϊ�� ![]() ��
��![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ