题目内容
【题目】图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图②的形状拼成一个正方形.
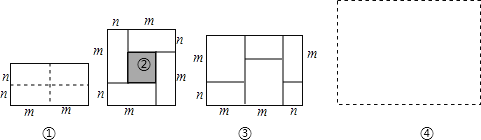
（1）请用两种不同的方法求图②中阴影部分的面积．
方法1：
方法2：
请你写出下列三个代数式： 
之间的等量关系．
；
（2）根据（1）题中的等量关系，解决如下问题：
已知： 
则
=
（3）实际上有许多代数恒等式可以用图形的面积来表示．如图③，它表示的代数恒等式是___ ．
（4）已知等式： 
，请你在图④中画出一个相应的几何图形。
【答案】（1）方法1： 
；方法2： 
； 
=
（2）1
（3）
（4）答案不唯一
【解析】试题分析：（1）表示出阴影部分的边长，然后利用正方形的面积公式列式；利用大正方形的面积减去四周四个矩形的面积列式；
（2）根据不同方法表示的阴影部分的面积相同解答；
（3）根据（2）的结论代入进行计算即可得解．
（4）要画的几何图形是一个长方形，长为（a+3），宽为：（a+1）．这个长方形有以下图形组成：一个边长为a的正方形，4个以a，1为长和宽的长方形，3个以1为边长的正方形．
试题解析：（1）方法1： 
方法2： 
请你写出下列三个代数式： 
之间的等量关系．
=
（2）1
（3）
（4）答案不唯一。如图，
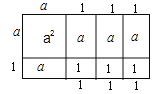
练习册系列答案
相关题目
