题目内容
已知二次函数y=x2－(2a+3)x+4a+2与x轴交于A、B两点，与y轴交于点C，并且点A在点B左侧，位于原点两侧. 若S△ABC的面积为3，求a的值.
.解：△=(2a+3)2－4(4a+2)=4a2－4a+1=(2a－1)2
∴
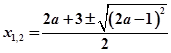
即x1=2a+1，x2="2. " ...………………………………………….1’
∵与x轴交点A在点B左侧，且位于原点两侧
∴A（2a+1,0），B（2,0）且2a+1<0.
∴AB=2－(2a+1)=1－2a. ...………………………………………….2’
∵与y轴交于点C，∴C（0，4a+2）
∴S△ABC=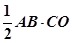
=
(1－2a) |4a+2|="3 " ...………………………………….3’
∴－(1－2a) (2a+1)="3 " 解得a="±1 " ...……………………………….4’
∵2a+1<0，∴a=－1. ...………………………………………….5
解析
练习册系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．