题目内容
函数y=1-|x-x2|的图象是
- A.

- B.

- C.

- D.

A
分析:通过对x-x2≤0与x-x2≥0的讨论,将y=1-|x-x2|中的绝对值符号去掉,转化为分段的二次函数,通过数形结合即可获得答案.
解答:解:∵y=1-|x-x2|= ,
,
∴当0≤x≤1,y=x2-x+1,其开口向上,对称轴为x= ,从而可排除D,B;
,从而可排除D,B;
同理,当x<0或x>1时,y=-x2+x+1,其开口向下,对称轴为x= ,从而可排除C,
,从而可排除C,
故选:A.
点评:本题考查了带绝对值的函数以及二次函数的图象与性质,通过对x-x2≤0与x-x2≥0的讨论去掉绝对值符号是关键,也是难点,属于中档题.
分析:通过对x-x2≤0与x-x2≥0的讨论,将y=1-|x-x2|中的绝对值符号去掉,转化为分段的二次函数,通过数形结合即可获得答案.
解答:解:∵y=1-|x-x2|=
 ,
,∴当0≤x≤1,y=x2-x+1,其开口向上,对称轴为x=
 ,从而可排除D,B;
,从而可排除D,B;同理,当x<0或x>1时,y=-x2+x+1,其开口向下,对称轴为x=
 ,从而可排除C,
,从而可排除C,故选:A.
点评:本题考查了带绝对值的函数以及二次函数的图象与性质,通过对x-x2≤0与x-x2≥0的讨论去掉绝对值符号是关键,也是难点,属于中档题.

练习册系列答案
相关题目
函数y=
中自变量x的取值范围是( )
| ||
| x |
A、x≤
| ||
B、x>-
| ||
| C、x≠0 | ||
D、x<
|
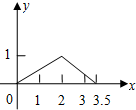
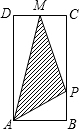 如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A?B?C?M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A?B?C?M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )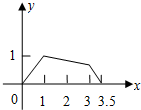


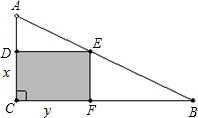 为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.
为60米和120米.现准备在AB上选一个点E,在空地中(如图所示)挖掘建造一个矩形游泳池.