题目内容
直角坐标平面内，一点光源位于A（0，5）处，线段CD⊥x轴，D为垂足，C（4，1），则CD在x轴上的影长为________，点C的影子的坐标为________．
1 （5，0）
分析：根据题意画出图形，点C在x轴上的影子为C′，由CD∥OA，得出相似三角形，利用相似比求CD在x轴上的影长DC′即可．
解答：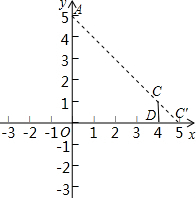
解：如图，设点C在x轴上的影子为C′，
∵CD∥OA，
∴△C′AO∽△C′CD，
∴
=
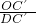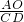，即
=
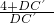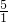，解得DC′=1，
OC′=OD+DC′=4+1=5，
∴点C的影子的坐标为（5，0）．
故答案为：1，（5，0）．
点评：本题考查了中心投影，坐标与图形的性质．关键是根据图形的特点，构造相似三角形，利用相似比求相关线段长．
分析：根据题意画出图形，点C在x轴上的影子为C′，由CD∥OA，得出相似三角形，利用相似比求CD在x轴上的影长DC′即可．
解答：
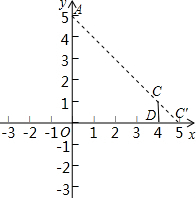解：如图，设点C在x轴上的影子为C′，∵CD∥OA，
∴△C′AO∽△C′CD，
∴
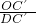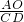=，即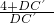=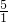，解得DC′=1，OC′=OD+DC′=4+1=5，
∴点C的影子的坐标为（5，0）．
故答案为：1，（5，0）．
点评：本题考查了中心投影，坐标与图形的性质．关键是根据图形的特点，构造相似三角形，利用相似比求相关线段长．
练习册系列答案
相关题目
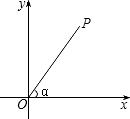如图，在直角坐标平面内有一点P（3，4），那么OP与x轴正半轴的夹角a的正弦值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|