题目内容
 如图,P为正方形ABCD内的一点,△ABP绕点B顺时针旋转得到△CBE,则∠PBE的度数是
如图,P为正方形ABCD内的一点,△ABP绕点B顺时针旋转得到△CBE,则∠PBE的度数是
- A.70°
- B.80°
- C.90°
- D.100°
C
分析:根据旋转的性质易得△ABP≌△CBE,进而可得∠ABP=∠CBE,又有∠ABP+∠PBC=90°,等量代换可得答案.
解答:根据旋转的意义,易得△ABP≌△CBE,
所以∠ABP=∠CBE,
而∠ABP+∠PBC=90°,
故∠CBE+∠PBC=90°,即∠PBE=90度.
故选C.
点评:此题主要考查了图形旋转的性质,难度不大.
【链接】旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.
分析:根据旋转的性质易得△ABP≌△CBE,进而可得∠ABP=∠CBE,又有∠ABP+∠PBC=90°,等量代换可得答案.
解答:根据旋转的意义,易得△ABP≌△CBE,
所以∠ABP=∠CBE,
而∠ABP+∠PBC=90°,
故∠CBE+∠PBC=90°,即∠PBE=90度.
故选C.
点评:此题主要考查了图形旋转的性质,难度不大.
【链接】旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以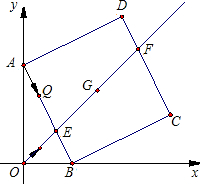 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.