题目内容
【题目】如图，抛物线y＝ax2﹣1（a＞0）与直线y＝kx+3交于MN两点，在y轴负半轴上存在一定点P，使得不论k取何值，直线PM与PN总是关于y轴对称，则点P的坐标是_____
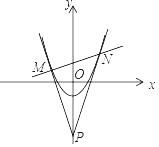
【答案】(0,-5)
【解析】
根据题意设M（xM，kxM+3），N（xN，kxN+3），P（0，t），然后根据抛物线与直线的交点得出一元二次方程，然后由根与系数的关系求得xM+xN＝
，xM×xN＝﹣
，再由相似三角形的判定和性质求得t，继而求得点P的坐标.
如图作MB⊥y轴，NA⊥y轴
∵M，N是直线y＝kx+3的点
∴设M（xM，kxM+3），N（xN，kxN+3），P（0，t）
∵抛物线y＝ax2﹣1（a＞0）与直线y＝kx+3交于MN两点
∴ax2﹣1＝kx+3
ax2﹣kx﹣4＝0
∴xM+xN＝，xM×xN＝﹣，
∵直线PM与PN总是关于y轴对称
∴∠MPA＝∠NPA，且∠MBP＝∠NAP＝90°
∴△MBP∽△NAP，
∴
即
，
∴（﹣xM﹣xN）（3﹣t）＝2kxMxN
∴﹣（3﹣t）＝2k×（-），
∴t＝﹣5
∴P（0，﹣5）.
故答案为（0，﹣5）
练习册系列答案
相关题目
