题目内容
已知连接三角形各边中点所得三角形的周长是10cm,则原三角形的周长为________cm.
20
分析:中点三角形的每边长等于原三角形各边的一半,所以原三角形的周长等于中点三角形周长的2倍.
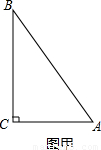
解答: 解:如图:
解:如图:
∵D、E、F分别是△ABC的AB、AC、BC边的中点,
∴DE= AC,EF=
AC,EF= AB,DF=
AB,DF= BC,
BC,
∴DE+EF+DF= (AB+BC+CD),
(AB+BC+CD),
即AB+BC+CD=2(DE+EF+DF)=2×10=20.
故答案为20.
点评:本题考查的是三角形中位线的性质,三角形的三条中位线把原三角形分成可重合的4个小三角形,因而每个小三角形的周长为原三角形周长的 .
.
分析:中点三角形的每边长等于原三角形各边的一半,所以原三角形的周长等于中点三角形周长的2倍.
解答:
 解:如图:
解:如图:∵D、E、F分别是△ABC的AB、AC、BC边的中点,
∴DE=
 AC,EF=
AC,EF= AB,DF=
AB,DF= BC,
BC,∴DE+EF+DF=
 (AB+BC+CD),
(AB+BC+CD),即AB+BC+CD=2(DE+EF+DF)=2×10=20.
故答案为20.
点评:本题考查的是三角形中位线的性质,三角形的三条中位线把原三角形分成可重合的4个小三角形,因而每个小三角形的周长为原三角形周长的
 .
. 
练习册系列答案
相关题目
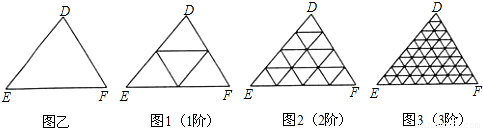
 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.