题目内容
 如图:已知AB∥CD,∠E=50°,那么∠B+∠F+∠D=________度.
如图:已知AB∥CD,∠E=50°,那么∠B+∠F+∠D=________度.
230
分析:分别过E,F做AB的平行线,使AB∥GH∥MN∥CD,根据平行线的性质可得到∠B=∠BEH,∠HEF=∠EFM,∠D+∠MFD=180°,已知∠BEH+∠HEF=∠E=50°,∠EFM+∠MFD=∠F,从而通过角之间的替换不难求得∠B+∠F+∠D的度数.
解答: 解:分别过E,F做AB的平行线,使AB∥GH∥MN∥CD
解:分别过E,F做AB的平行线,使AB∥GH∥MN∥CD
∵AB∥GH∥MN∥CD
∴∠B=∠BEH,∠HEF=∠EFM,∠D+∠MFD=180°
∵∠BEH+∠HEF=∠E=50°,∠EFM+∠MFD=∠F
∴∠B+∠F+∠D=∠BEF+∠HEF+∠MFD+∠D=(∠BEF+∠HEF)+(∠MFD+∠D)=50°+180°=230°
故答案为:230°
点评:此题主要考查学生对平行线的性质的掌握情况,关键是辅助线的作法.
分析:分别过E,F做AB的平行线,使AB∥GH∥MN∥CD,根据平行线的性质可得到∠B=∠BEH,∠HEF=∠EFM,∠D+∠MFD=180°,已知∠BEH+∠HEF=∠E=50°,∠EFM+∠MFD=∠F,从而通过角之间的替换不难求得∠B+∠F+∠D的度数.
解答:
 解:分别过E,F做AB的平行线,使AB∥GH∥MN∥CD
解:分别过E,F做AB的平行线,使AB∥GH∥MN∥CD∵AB∥GH∥MN∥CD
∴∠B=∠BEH,∠HEF=∠EFM,∠D+∠MFD=180°
∵∠BEH+∠HEF=∠E=50°,∠EFM+∠MFD=∠F
∴∠B+∠F+∠D=∠BEF+∠HEF+∠MFD+∠D=(∠BEF+∠HEF)+(∠MFD+∠D)=50°+180°=230°
故答案为:230°
点评:此题主要考查学生对平行线的性质的掌握情况,关键是辅助线的作法.

练习册系列答案
相关题目
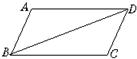 15、如图,已知AB=CD且∠ABD=∠BDC,要证∠A=∠C,判定△ABD≌△CDB的方法是( )
15、如图,已知AB=CD且∠ABD=∠BDC,要证∠A=∠C,判定△ABD≌△CDB的方法是( )
 如图,已知AB∥CD,∠1=50°25′,则∠2的大小是
如图,已知AB∥CD,∠1=50°25′,则∠2的大小是 如图,已知 AB∥CD,∠A=53°,则∠1的度数是
如图,已知 AB∥CD,∠A=53°,则∠1的度数是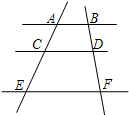 如图,已知AB∥CD∥EF,那么下列结论中,正确的是( )
如图,已知AB∥CD∥EF,那么下列结论中,正确的是( )