题目内容
 设一次函数y=
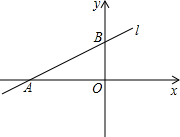
设一次函数y= x+2的图象为直线l,l与x轴、y轴分别交于点A、B.
x+2的图象为直线l,l与x轴、y轴分别交于点A、B.
求tan∠BAO的值.
解:在一次函数y= x+2中,令x=0,解得y=2;
x+2中,令x=0,解得y=2;
令y=0,解得x=-4.
因而A,B的坐标是(-4,0),(0,2).
则OA=4,OB=2,
因而tan∠BAO= =
= =
= .
.
分析:在一次函数中,求出函数与坐标轴的交点坐标,就可以求出OA,OB的长,就可以求出三角函数值.
点评:本题主要考查了函数与坐标轴的交点的求法,以及正切函数的定义.
 x+2中,令x=0,解得y=2;
x+2中,令x=0,解得y=2;令y=0,解得x=-4.
因而A,B的坐标是(-4,0),(0,2).
则OA=4,OB=2,
因而tan∠BAO=
 =
= =
= .
.分析:在一次函数中,求出函数与坐标轴的交点坐标,就可以求出OA,OB的长,就可以求出三角函数值.
点评:本题主要考查了函数与坐标轴的交点的求法,以及正切函数的定义.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 设一次函数
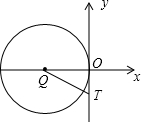
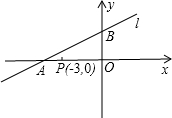
设一次函数 如图,设一次函数y=x-1的图象记为直线l,△ABC三个顶点的坐标分别为C(1,1),B(5,1),A(1,4).解决下列问题:
如图,设一次函数y=x-1的图象记为直线l,△ABC三个顶点的坐标分别为C(1,1),B(5,1),A(1,4).解决下列问题: 阅读下面的材料:
阅读下面的材料: