Question

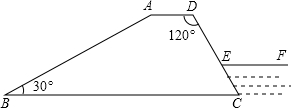
如图，某水库大坝的横断面为梯形ABCD，坝顶宽5米，坝高5

3

米，斜坡AB的坡度i=1﹕

3

，坡角∠B=45°．求：
（1）坡角α的度数；
（2）坝底AB的长度．

Answer 1

分析：（1）先过点D、C作梯形的高DE、CF，根据正切求出α的度数即可；
（2）在Rt△ADE中，根据DE=5

3

，α=30°，求出AE，在Rt△CBF中，再根据∠B=45°，得出BF=CF=5

3

，最后根据AB=AE+EF+BF，代入计算即可．

解答：解：（1）过点D、C作梯形的高DE、CF，
∵tanα=

1

3

=

3

3

，
∴α=30°，
答：坡角α的度数为30°．

（2）在Rt△ADE中，
∵DE=5

3

，α=30°，
∴AE=

3

•DE=

3

×5

3

=15，
在Rt△CBF中，
∵∠B=45°，
∴BF=CF=5

3

，
∴AB=AE+EF+BF=15+5+5

3

=（20+5

3

）米，
答：坝底AB的长为20+5

3

米．

点评：此题考查了解直角三角形的应用，通过构造直角三角形和矩形，利用坡角，坡度的概念求解．