题目内容
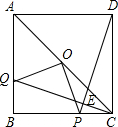
如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于 点P,连接OP,OQ;
点P,连接OP,OQ;
求证:
(1)△BCQ≌△CDP;
(2)OP=OQ.
证明:
(1)∵四边形ABCD是正方形,
∴∠B=∠PCD=90°,BC=CD,
∴∠2+∠3=90°,
又∵DP⊥CQ,
∴∠2+∠1=90°,
∴∠1=∠3,
在△BCQ和△CDP中,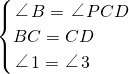 .
.
∴△BCQ≌△CDP.
(2)连接OB.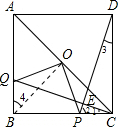
由(1):△BCQ≌△CDP可知:BQ=PC,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
而点O是AC中点,
∴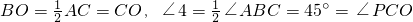 ,
,
在△BOQ和△CDP中,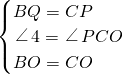 .
.
∴△BOQ≌△COP,
∴OQ=OP.
分析:(1)根据正方形的性质和DP⊥CQ于点E可以得到证明△BCQ≌△CDP的全等条件;
(2)根据(1)得到BQ=PC,然后连接OB,根据正方形的性质可以得到证明△BOQ≌△COP的全等条件,然后利用全等三角形的性质就可以解决题目的问题.
点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,利用它们构造证明全等三角形的条件,然后通过全等三角形的性质解决问题.

练习册系列答案
相关题目
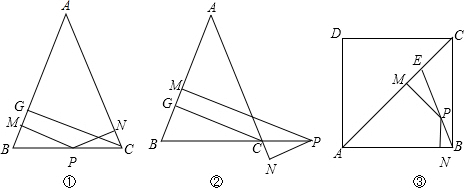 .
. 14、如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
14、如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
 点P,连接OP,OQ;
点P,连接OP,OQ; 如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.