题目内容
 如图,A、C在⊙O上,以OA为直径的⊙P交PC于B,且∠OAB=45°,OA=4,则弧AB、弧AC和线段BC所围的阴影部分的面积S=
如图,A、C在⊙O上,以OA为直径的⊙P交PC于B,且∠OAB=45°,OA=4,则弧AB、弧AC和线段BC所围的阴影部分的面积S=| 5π |
| 3 |
| 3 |
| 5π |
| 3 |
| 3 |
分析:根据∠OAB=45°可以发现CP⊥OA.则阴影部分的面积等于直角三角形APC的面积减去扇形PAB的面积,连接OC、AC.根据线段垂直平分线的性质得到OC=OA,即可发现等边三角形AOC,从而求得∠A=60°,再由阴影部分的面积=S扇形OAC-S△OPC-S扇形PAB即可得出答案.
解答:解:连接OC、AC,

∵PA=PB,∠OAB=45°,
∴∠APB=90°,
又OP=AP,
∴OC=AC.
又OA=OC,
∴△AOC是等边三角形.
∴∠A=60°.
∵PA=2,
∴PC=2
.
∴阴影部分的面积=S扇形OAC-S△OPC-S扇形PAB=
-2
.
故答案为:
-2
.

∵PA=PB,∠OAB=45°,
∴∠APB=90°,
又OP=AP,
∴OC=AC.
又OA=OC,
∴△AOC是等边三角形.
∴∠A=60°.
∵PA=2,
∴PC=2
| 3 |
∴阴影部分的面积=S扇形OAC-S△OPC-S扇形PAB=
| 5π |
| 3 |
| 3 |
故答案为:
| 5π |
| 3 |
| 3 |
点评:本题考查了扇形的面积计算,解答本题的关键是发现此题中的等腰直角三角形和等边三角形,有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
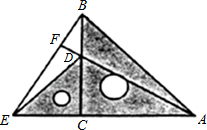 把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.试判断AF和BE的位置关系,并说明理由.
把两个含有45°角的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.试判断AF和BE的位置关系,并说明理由. 如图,是一个挂在墙壁上时钟的示意图.O是其秒针的转动中心,M是秒针的另一端,OM=8cm,l是过点O的铅直直线.现有一只蚂蚁P在秒针OM上爬行,蚂蚁P到点O的距离与M到l的距离始终相等.则1分钟的时间内,蚂蚁P被秒针OM携带的过程中移动的路程(非蚂蚁在秒针上爬行的路程)是
如图,是一个挂在墙壁上时钟的示意图.O是其秒针的转动中心,M是秒针的另一端,OM=8cm,l是过点O的铅直直线.现有一只蚂蚁P在秒针OM上爬行,蚂蚁P到点O的距离与M到l的距离始终相等.则1分钟的时间内,蚂蚁P被秒针OM携带的过程中移动的路程(非蚂蚁在秒针上爬行的路程)是
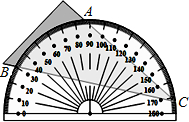 如图,三角形纸板放置在量角器上,三角形的顶点点C恰在半圆上,两边与半圆的交点记为A、B,A点的读数为86°,B点的读数为30°,则∠ACB的大小为
如图,三角形纸板放置在量角器上,三角形的顶点点C恰在半圆上,两边与半圆的交点记为A、B,A点的读数为86°,B点的读数为30°,则∠ACB的大小为 如图是小明同学在体育课上跳远后留下的脚印,则表示他的跳远成绩是( )
如图是小明同学在体育课上跳远后留下的脚印,则表示他的跳远成绩是( )