题目内容
如图，已知?ABCD的面积为24，E，F分别是BC，CD的中点，那么△AEF的面积为________．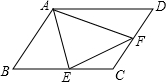
9
分析：根据已知条件，分别求出△ABE、△EFC、△AFD的面积，即可求出△AEF的面积．
解答：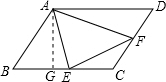
解：作?ABCD的高线AG，则BC×AG=24，
∵E，F分别是BC，CD的中点
∴S△ABE=
×
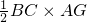=6，
S△ADF=BC×AG=6，
S△CEF=×BC×AG=3
∴△AEF的面积=24-6-6-3=9．
故答案为9．
点评：此题的关键是由已知的三角形面积求出被分割的三角形的面积，然后由总面积减那三个小面积就是所求的面积．
分析：根据已知条件，分别求出△ABE、△EFC、△AFD的面积，即可求出△AEF的面积．
解答：
解：作?ABCD的高线AG，则BC×AG=24，∵E，F分别是BC，CD的中点
∴S△ABE=
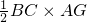×=6，S△ADF=
BC×AG=6，S△CEF=
×BC×AG=3∴△AEF的面积=24-6-6-3=9．
故答案为9．
点评：此题的关键是由已知的三角形面积求出被分割的三角形的面积，然后由总面积减那三个小面积就是所求的面积．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14、如图，已知?ABCD中，AB=4，BC=6，BC边上的高AE=2，则DC边上的高AF的长是
26、如图，已知?ABCD，AE平分∠BAD，交DC于E，DF⊥BC于F，交AE于G，且DF=AD．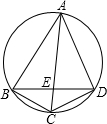
如图，已知ABCD是圆的内接四边形，对角线AC和BD相交于E，BC=CD=4，AE=6，如果线段BE和DE的长都是整数，则BD的长等于
如图，已知ABCD是圆O的内接四边形，AB=BD，BM⊥AC于M，求证：AM=DC+CM．