Question

（本题满分12分）
已知直线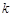（＜0）分别交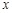轴、轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作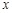轴的垂线交直线AB于点C，设运动时间为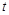秒．

（1）当时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时两点同时停止运动（如图1）．
①直接写出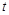＝1秒时C、Q两点的坐标；
②若以Q、C、A为顶点的三角形与△AOB相似，求的值．
（2）当时，设以C为顶点的抛物线与直线AB的另一交点为D
（如图2），①求CD的长；
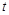②设△COD的OC边上的高为，当为何值时，的值最大？

Answer 1

（1）①C（1，2），Q（2，0）．                         ……..2分
②由题意得：P(t，0)，C(t，－ｔ＋3)，Q(3－t，0)，
分两种情形讨论：
情形一：当△AQC∽△AOB时，∠AQC=∠AOB＝90°，3－t=t，∴t=1.5．
情形二：当△ACQ∽△AOB时，∠ACQ=∠AOB＝90°，t =2（－t＋3），∴t=2．
∴满足条件的t的值是1.5秒或2秒．                        ……6分
(2) ①由题意得：C(t，－＋3)，∴以C为顶点的抛物线解析式是，
由，解得x₁=t，x₂=t；过点D作DE⊥CP于点E
△DEC∽△AOB，∴， CD=．…….9分
②∵CD=，CD边上的高=．∴S_△COD=．∴S_△COD为定值；
要使OC边上的高h的值最大，只要OC最短．因为当OC⊥AB时OC最短，此时OC的长为。Rt△PCO∽Rt△OAB，∴，OP=，即t=，∴当t为秒时，h的值最大．                     …….12分

解析