题目内容
如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点,连接QP并延长交CB的延长线于点D.

(1)判断直线PQ与⊙O的位置关系,并说明理由:
(2)若AP=4,tanA= ,
,
①求⊙O的半径的长;
②求PD的长.
(1)直线PQ与⊙O相切.理由见解析;(2)① ;②
;② .
.
【解析】
试题分析:(1)首先连接OP、CP,由BC是⊙O的直径,根据圆周角定理可得∠BPC=90°,又由Q是AC的中点,根据直角三角形中,斜边上的中线等于斜边的一半,即可求得PQ=CQ=AQ,继而可证得∠1+∠3=90°,则可得直线PQ与⊙O相切;
(2)在Rt△APC中利用三角函数求出PC和AC的长;在Rt△ABC中求出BC的长即可确定圆的半径;
(3)连接OQ,易证△DOQ∽△DBP,得 ,即
,即 ,又BP=1,PQ=
,又BP=1,PQ= AC=
AC= ,从而可求PD的长.
,从而可求PD的长.
试题解析:(1)直线PQ与⊙O相切.理由如下:
连接OP、CP.

∵BC是⊙O的直径,
∴∠BPC=90°.
又∵Q是AC的中点,
∴PQ=CQ=AQ.
∴∠3=∠4,
∵∠BCA=90°,
∴∠2+∠4=90°.
∵∠1=∠2,
∴∠1+∠3=90°.
即∠OPQ=90°,
∴直线PQ与⊙O相切;
(2)①在Rt△APC中,AP=4,tanA=
∴CP=AP×tanA=4× =2
=2
∴AC=
在Rt△ABC中,AC= ,tanA=
,tanA=
∴BC=AC×tanA= ×
× =
=
即⊙O的半径长为
(3)连接OQ

∵Q是AC的中点,O是BC的中点
∴OQ∥AB,OQ= AB=
AB=
∴△DOQ∽△DBP
∴
即:
又BP=1,PQ= AC=
AC=
∴
即:PD=
考点:1.切线的判定;2.相似三角形的性质与判定.
考点分析: 考点1:圆 圆,圆的有关性质与圆的有关计算是近几年各地中考命题的重点内容。题型以填空题,选择题和解答题为主,也有以阅读理解,条件开放,结论开放探索题作为新的题型,分值一般是6-12分,难易度为中,考察内容:①圆的有关性质的应用。垂径定理是重点。② 直线和圆,圆和圆的位置关系的判定及应用。③弧长,扇形面积,圆柱,圆锥的侧面积和全面积的计算④圆与相似三角形,三角函数的综合运用以及有关的开放题,探索题。突破方法:①熟练掌握圆的有关行政,掌握求线段,角的方法,理解概念之间的相互联系和知识之间的相互转化。②理解直线和原的三种位置关系,掌握切线的性质和判定的歌,会根据条件解决圆中的动态问题。③掌握有两圆半径的和或差与圆心距的大小关系来盘底的那个两个圆的位置关系,对中考试题中常出现的阅读理解题,探索题,要灵活运用圆的有关性质,进行合理推理与计算。④掌握弧长,扇形面积计算公式。⑤理解圆柱,圆锥的侧面展开图⑥对组合图形 的计算要灵活运用计算方法解题。 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的和是
的和是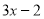 ,则这个多项式为( )
,则这个多项式为( ) (B)
(B)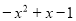
 (D)
(D)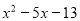

 亿元 B、
亿元 B、 亿元
亿元 亿元 D、
亿元 D、 亿元
亿元
