题目内容
（2008•西藏）如图，PA、PB是⊙O的两条切线，切点是A、B，如果OP=2，PA=| 3 |
分析：由切线长定理知△APO≌△BPO，得∠AOP=∠BOP．可求得sin∠AOP=
：2，所以可知∠AOP=60°，从而求得∠AOB的值．
| 3 |
解答：解：∵PA、PB是⊙O的两条切线，切点是A、B，
∴PA=PB，∠PAO=∠PBO=90°，
∴在Rt△APO与Rt△BPO中，
，
∴Rt△APO≌Rt△BPO（HL），
∴∠AOP=∠BOP．
∵sin∠AOP=AP：OP=2
：4=
：2，
∴∠AOP=60°．
∴∠AOB=2∠AOP=120°．
故选D．
∴PA=PB，∠PAO=∠PBO=90°，
∴在Rt△APO与Rt△BPO中，
|
∴Rt△APO≌Rt△BPO（HL），
∴∠AOP=∠BOP．
∵sin∠AOP=AP：OP=2
| 3 |
| 3 |
∴∠AOP=60°．
∴∠AOB=2∠AOP=120°．
故选D．
点评：本题考查了切线的性质．解题时，要熟记特殊角的三角函数值．
练习册系列答案
相关题目
（2008•西藏）拉萨市某风景区，在2007年“五一”长假期间，接待游人情况如下图所示，则这7天游览该风景区的平均人数为（ ）
（2008•西藏）如图所示，在平面直角坐标系内，正比例函数y=x和一次函数y=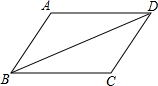
（2008•西藏）如图，已知?ABCD，按要求完成下列各题．
（2008•西藏）已知：如图，AB是⊙O的直径．OD⊥AB．交⊙O于点F，点C是⊙O上一点，连接OC、AC、BC．AC的延长线交OD于点D，BC交OD于点E．