题目内容
【题目】如图,在Rt△ABC中,∠A=30°,BC=2 ![]() ,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )
,以直角边AC为直径作⊙O交AB于点D,则图中阴影部分的面积是( )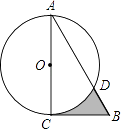
A.![]() ﹣
﹣ ![]()
B.![]() ﹣
﹣ ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
【答案】A
【解析】解:如图连接OD、CD. 
∵AC是直径,
∴∠ADC=90°,
∵∠A=30°,
∴∠ACD=90°﹣∠A=60°,
∵OC=OD,
∴△OCD是等边三角形,
∵BC是切线.
∴∠ACB=90°,∵BC=2 ![]() ,
,
∴AB=4 ![]() ,AC=6,
,AC=6,
∴S阴=S△ABC﹣S△ACD﹣(S扇形OCD﹣S△OCD)
= ![]() ×6×2
×6×2 ![]() ﹣
﹣ ![]() ×3×
×3× ![]() ﹣(
﹣( ![]() ﹣
﹣ ![]() ×32)
×32)
= ![]() ﹣
﹣ ![]() π.
π.
所以答案是:A.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目