题目内容
(2009•淄博)如图,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,利用函数图象判断不等式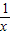 <kx+b的解集为( )
<kx+b的解集为( )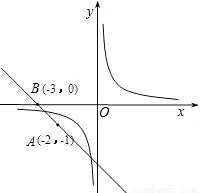
A.
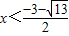 或
或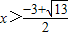
B.
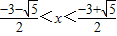
C.

D.
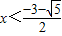 或
或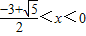
【答案】分析:直线y=kx+b经过A(-2,-1)和B(-3,0)两点,则利用待定系数法求得k,b的值,得到函数的解析式是y=-x-3,得到这个函数与y= 的交点的横坐标,再根据图象可以得到不等式
的交点的横坐标,再根据图象可以得到不等式 <kx+b的解集.
<kx+b的解集.
解答:解:直线y=kx+b经过A(-2,-1)和B(-3,0)两点,
则 解得,解得
解得,解得 ,
,
因此函数的解析式是y=-x-3,
这个函数与y= 的交点的横坐标是
的交点的横坐标是 ,
,
根据图象可以得到,不等式 <kx+b的解集为
<kx+b的解集为 或
或 .
.
故选D.
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.
 的交点的横坐标,再根据图象可以得到不等式
的交点的横坐标,再根据图象可以得到不等式 <kx+b的解集.
<kx+b的解集.解答:解:直线y=kx+b经过A(-2,-1)和B(-3,0)两点,
则
 解得,解得
解得,解得 ,
,因此函数的解析式是y=-x-3,
这个函数与y=
 的交点的横坐标是
的交点的横坐标是 ,
,根据图象可以得到,不等式
 <kx+b的解集为
<kx+b的解集为 或
或 .
.故选D.
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
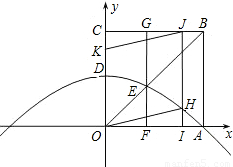 (2009•淄博)如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.
(2009•淄博)如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点. <kx+b的解集为( )
<kx+b的解集为( )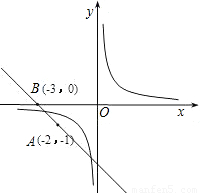
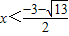 或
或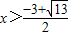

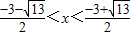
 或
或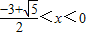
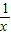 <kx+b的解集为( )
<kx+b的解集为( )
 或
或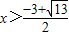

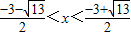
 或
或
 (2009•淄博)如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.
(2009•淄博)如图,在平面直角坐标系中,正方形OABC的边长是2.O为坐标原点,点A在x的正半轴上,点C在y的正半轴上.一条抛物线经过A点,顶点D是OC的中点.