题目内容
如图，l1∥l2，∠1=120°，∠2=100°，则∠3=________度．
40
分析：过点A作l1的平行线，根据平行线的性质，即可求解．
解答：
解：过点A作AB∥l1，则l1∥AB∥l2．
∴∠1+∠CAB=180°，
∴∠BAC=180°-120°=60°．
∴∠DAB=∠2-∠BAC=100°-60°=40°．
∵AB∥l2
∴∠3=∠DAB=40°．
故答案为：40．
点评：本题主要考查了平行线的性质，两直线平行，内错角相等，同旁内角互补．正确作出辅助线是解题的关键．
分析：过点A作l1的平行线，根据平行线的性质，即可求解．
解答：
解：过点A作AB∥l1，则l1∥AB∥l2．∴∠1+∠CAB=180°，
∴∠BAC=180°-120°=60°．
∴∠DAB=∠2-∠BAC=100°-60°=40°．
∵AB∥l2
∴∠3=∠DAB=40°．
故答案为：40．
点评：本题主要考查了平行线的性质，两直线平行，内错角相等，同旁内角互补．正确作出辅助线是解题的关键．
练习册系列答案
相关题目
13、如图，l1∥l2，∠1=120°，∠2=100°，则∠3=（ ）
如图，l1∥l2，AB⊥AC，∠ABC=50°，则∠1=（ ）度．
如图，l1∥l2∥l3，已知L1与l3之间的距离为8cm，l1与l2之间的距离为3cm，则l2与l3之间的距离为
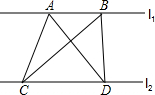如图，l1∥l2，A、B为直线l1上两点，C、D为直线l2上两点，则△ACD与△BCD的面积大小关系是（ ）| A、S△ACD＜S△BCD | B、S△ACD=S△BCD | C、S△ACD＞S△BCD | D、不能确定 |