题目内容
如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点D处，点A落在点
处，连结BE．
求证：四边形
是菱形；
若AB =" 4" cm，BC =" 8" cm，求折痕EF的长．
证明：(1) ∵ 四边形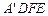
与四边形ABFE关于EF成轴对称
∴ 
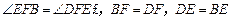
又∵ 矩形ABCD
∴ 
∴ 
∴ 
∴ 
∴ 
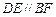
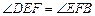
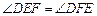
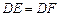
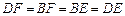
∴ 四边形BEDF是菱形
(2) 连结BD，交EF于点O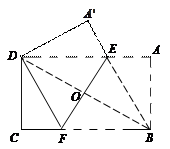
∵ 四边形BEDF是菱形
∴ DB = BF
设DF =" BF" = x
则CF =" BC" – BF =" 8" – x
在Rt△DCF中，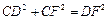
即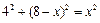 
∴ x = 5
∴ DF =" BF" = 5
∴ CF = 3
∵ EF垂直平分BD
∴ 
∵ 
∴ 
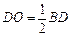
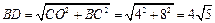
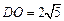
在Rt△DOF中
∴ 
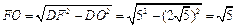
∴ EF =" 2FO" =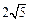
解析
练习册系列答案
名校课堂系列答案
相关题目
22、如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处；
（2009•自贡）如图，把矩形纸片ABCD沿EF折叠，使点B落在AD边上的点B′处，点A落在A′处．
如图，把矩形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．
如图，把矩形纸片ABCD沿着EF折叠，使点B落在边AD上的点D处．点A落在点A′．
10、如图，把矩形纸片ABCD沿EF折叠，使点B落在AD边上的点B′处，点A落在点A′处．设AE=a，AB=b，BF=c，下列结论：