题目内容
若点A的坐标为(3,4),⊙A的半径5,则点P(6,3)的位置为( )
| A、P在⊙A内 | B、P在⊙A上 | C、P在⊙A外 | D、无法确定 |
分析:作辅助线构成直角三角形,通过勾股定理将AP的长求出,然后与⊙A的半径进行比较来确定点P与⊙A的位置关系.
若AP的长大于半径,则P在⊙A外;
若AP的长等于半径,则P在⊙A上;
若AP的长小于半径,则P在⊙A内.
若AP的长大于半径,则P在⊙A外;
若AP的长等于半径,则P在⊙A上;
若AP的长小于半径,则P在⊙A内.
解答:解:画出平面直角坐标系中A点和P点,连接AP,过A点作x轴的垂线,过P点作y轴的垂线交于B点,
则AB=4-3=1,BP=6-3=3.
在直角三角形ABP中,根据勾股定理AP=
=
<5,
故P在⊙A内.
故选A.
则AB=4-3=1,BP=6-3=3.
在直角三角形ABP中,根据勾股定理AP=
| 12+32 |
| 10 |
故P在⊙A内.
故选A.
点评:本题运用勾股定理将AP的长求出,然后与半径的长进行比较,从而确定点与圆的位置关系.

练习册系列答案
相关题目
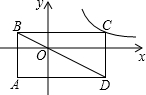 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数 25、如图,在平面直角坐标系中,O为坐标原点,二次函数y=x2+bx+c的图象与x轴相交于点A、B,与y轴的负半轴相交于点C,若点C的坐标为(0,-3),且BO=CO,
25、如图,在平面直角坐标系中,O为坐标原点,二次函数y=x2+bx+c的图象与x轴相交于点A、B,与y轴的负半轴相交于点C,若点C的坐标为(0,-3),且BO=CO,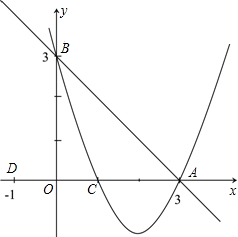 (2012•铜仁地区)如图已知:直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(2012•铜仁地区)如图已知:直线y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.