题目内容
已知A、B是⊙O上两点,点P是⊙O上的动点(P不与A、B重合),⊙O的半径为1,AB= ,则∠APB的度数是________.
,则∠APB的度数是________.
45°或135°
分析:由OA=OB=1,AB= ,根据勾股定理的逆定理得到∠AOB=90°,分类讨论:当点在优弧AB上,根据圆周角定理得到∠AP1B=
,根据勾股定理的逆定理得到∠AOB=90°,分类讨论:当点在优弧AB上,根据圆周角定理得到∠AP1B= ∠AOB=45°;当点在弧AB上,根据圆内接四边形的性质得∠AP2B=180°-∠AP1B=135°.
∠AOB=45°;当点在弧AB上,根据圆内接四边形的性质得∠AP2B=180°-∠AP1B=135°.
解答:如图,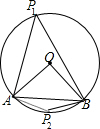
∵OA=OB=1,AB= ,
,
∴OA2+OB2=AB2,
∴∠AOB=90°,
当点在优弧AB上,则∠AP1B= ∠AOB=45°,
∠AOB=45°,
当点在弧AB上,则∠AP2B=180°-∠AP1B=180°-45°=135°,
∴∠APB的度数是45°或135°.
故答案为45°或135°.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
分析:由OA=OB=1,AB=
 ,根据勾股定理的逆定理得到∠AOB=90°,分类讨论:当点在优弧AB上,根据圆周角定理得到∠AP1B=
,根据勾股定理的逆定理得到∠AOB=90°,分类讨论:当点在优弧AB上,根据圆周角定理得到∠AP1B= ∠AOB=45°;当点在弧AB上,根据圆内接四边形的性质得∠AP2B=180°-∠AP1B=135°.
∠AOB=45°;当点在弧AB上,根据圆内接四边形的性质得∠AP2B=180°-∠AP1B=135°.解答:如图,

∵OA=OB=1,AB=
 ,
,∴OA2+OB2=AB2,
∴∠AOB=90°,
当点在优弧AB上,则∠AP1B=
 ∠AOB=45°,
∠AOB=45°,当点在弧AB上,则∠AP2B=180°-∠AP1B=180°-45°=135°,
∴∠APB的度数是45°或135°.
故答案为45°或135°.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
相关题目
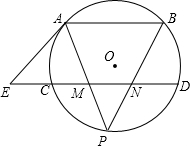 如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧
如图,已知AB、CD是⊙O的两条平行弦,过A点的⊙O的切线AE和DC的延长线交于E点,P为弧

 如图,已知OA、OB是⊙O的两条半径,C、D为OA、OB上的两点,且AC=BD.求证:AD=BC.
如图,已知OA、OB是⊙O的两条半径,C、D为OA、OB上的两点,且AC=BD.求证:AD=BC.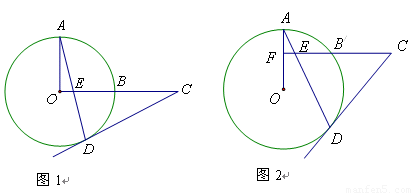
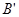 ,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?