题目内容
如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西600的方向,从B测得小船在北偏东450的方向.

(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到达点C处.此时,从B测得小船在北偏西150的方向.求点C与点B之间的距离.
(上述2小题的结果都保留根号)
【答案】
解:(1)如图,过点P作PD⊥AB于点D,

设PD=x,
由题意可知 ,PBD=450,∠PAD=300,
∴在Rt△BDP中,BD=PD= x。
在Rt△PDA中,AD= PD=
PD= 。
。
∵AB=2,∴ 。
。
解得 。
。
∴点P到海岸线l的距离为 km。
km。
(2)如图,过点B作BF⊥CA于点F,
在Rt△ABF中, ,
,
在Rt△ABC中,∠C=1800-∠BAC-∠ABC=450,
∴在Rt△BFC中, 。
。
∴点C与点B之间的距离为 。
。
【解析】
试题分析:(1)过点P作PD⊥AB于点D,构造直角三角形BDP和PDA,PD即为点P到海岸线l的距离,应用锐角三角函数即可求解。
(2)过点B作BF⊥CA于点F,构造直角三角形ABF和BFC,应用锐角三角函数即可求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
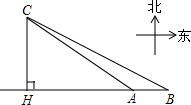 如图,在一笔直的海岸线上有A、B两个观测站,B在A的正东方向,AB=10千米,在某一时刻,从观测站A测得一艘集装箱货船位于北偏西62.6°的C处,同时观测站B测得改集装箱船位于北偏西69.2°方向,问此时该集装箱船与海岸之间距离CH约多少千米?(最后结果保留整数)
如图,在一笔直的海岸线上有A、B两个观测站,B在A的正东方向,AB=10千米,在某一时刻,从观测站A测得一艘集装箱货船位于北偏西62.6°的C处,同时观测站B测得改集装箱船位于北偏西69.2°方向,问此时该集装箱船与海岸之间距离CH约多少千米?(最后结果保留整数)