题目内容
规定符号[x]表示不超过x的最大整数,例[3.1]=3,[-
]=-3,[6]=6,求:方程2-x2=[x]大于-3的x的解
| 7 |
| 3 |
∵2-x2≤2,∴[x]≤2;又由x>-3,∴[x]≥-3,即:-3≤[x]≤2(6分)
当[x]=-3时,原方程化为2-x2=-3,∴x=±
,检验x=-
适合(8分)
当[x]=-2时,原方程化为2-x2=-2,∴x=±2,检验x=-2适合(10分)
当[x]=-1时,原方程化为2-x2=-1,∴x=±
,检验都不适合(12分)
当[x]=0时,原方程化为2-x2=0,∴x=±
,检验都不适合(14分)
当[x]=1时,原方程化为2-x2=1,∴x=±1,检验x=1适合(16分)
当[x]=2时,原方程化为2-x2=2,∴x=0,检验不适合(18分)
综上可得满足条件的方程的解为x=-
或x=-2或x=1.(20分)
当[x]=-3时,原方程化为2-x2=-3,∴x=±
| 5 |
| 5 |
当[x]=-2时,原方程化为2-x2=-2,∴x=±2,检验x=-2适合(10分)
当[x]=-1时,原方程化为2-x2=-1,∴x=±
| 3 |
当[x]=0时,原方程化为2-x2=0,∴x=±
| 2 |
当[x]=1时,原方程化为2-x2=1,∴x=±1,检验x=1适合(16分)
当[x]=2时,原方程化为2-x2=2,∴x=0,检验不适合(18分)
综上可得满足条件的方程的解为x=-
| 5 |

练习册系列答案
相关题目
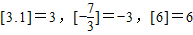 ,求:方程2-x2=[x]大于-3的x的解
,求:方程2-x2=[x]大于-3的x的解