题目内容
 如图AB是⊙O的直径,弦CD⊥AB于P,CD=4
如图AB是⊙O的直径,弦CD⊥AB于P,CD=4| 3 |
分析:连接OC,由直径AB垂直于弦CD,利用垂径定理得到P为CD的中点,由CD的长求出CP的长,在直角三角形OCP中,由OP与PC的长,利用勾股定理求出OC的长,即为OA的长,由AO+OP求出AP的长,在直角三角形ACP中,由AP与PC的长,利用勾股定理即可求出AC的长.
解答: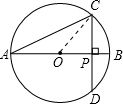 解:连接OC,如图所示:
解:连接OC,如图所示:
∵直径AB⊥CD,CD=4
,
∴P为CD的中点,即CP=DP=2
,
在Rt△OCP中,OP=2,CP=2
,
根据勾股定理得:OC=
=4,
则OA=OC=4,
则AP=AO+OP=4+2=6,
在Rt△APC中,AP=6,CP=2
,
根据勾股定理得:AC=
=4
.
故选C.
 解:连接OC,如图所示:
解:连接OC,如图所示:∵直径AB⊥CD,CD=4
| 3 |
∴P为CD的中点,即CP=DP=2
| 3 |
在Rt△OCP中,OP=2,CP=2
| 3 |
根据勾股定理得:OC=
| OP2+CP2 |
则OA=OC=4,
则AP=AO+OP=4+2=6,
在Rt△APC中,AP=6,CP=2
| 3 |
根据勾股定理得:AC=
| AP2+CP2 |
| 3 |
故选C.
点评:此题考查了垂径定理,以及勾股定理,熟练掌握定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
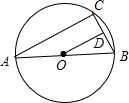 如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
 CF交AB于点M,连接DF并延长交BA的延长线于点N.
CF交AB于点M,连接DF并延长交BA的延长线于点N. 如图AB是⊙O的直径,∠D=35°,则∠AOC=
如图AB是⊙O的直径,∠D=35°,则∠AOC= (2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C. (2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.